Question

How do you find the reference angle $\theta ={{203}^{\circ }}$ and sketch the angle in standard position?

Answer 1

Hint: In this question, we have to find the reference angle and then sketch the angle. Thus, we will use the angle formula to get the solution. As we know, the reference angle is that acute angle with the x-axis and the terminal side of the angle. Thus, we know that $\theta ={{203}^{\circ }}$, thus it must lie after 180 degree and before 270 degree, which implies for the reference angle, we will subtract theta and 180 degree. In the last, we will sketch the angle using angle-radian formula, to get the required solution for the problem.

Complete step by step solution:
According to the problem, we have to find the value of the reference angle and sketch the given angle.
Thus, we will use the angle-radian formula to get the solution.
The angle given to us is $\theta ={{203}^{\circ }}$ ---------- (1)
As we know, the reference angle is the acute angle with the x-axis. Thus, we know that the given angle is greater than 180 degree, thus we will subtract the given angle and the 180 degree, which is
$\Rightarrow {{203}^{\circ }}-{{180}^{\circ }}$
$\Rightarrow {{23}^{\circ }}$ is the reference angle.
Now, we will sketch the given angle that is $\theta ={{203}^{\circ }}$in the standard form, thus we know that the given angle is greater than 180 degree. Also, there are four quadrants in the cartesian form, where first quadrant lies between 0 degree and 90 degree, second quadrant lies between 90 degree to 180 degree, and so on adding 90 degree to every quadrant, we get

Now, we see that angle 203 lies between 180 and 270 degree, thus the graph is equal to

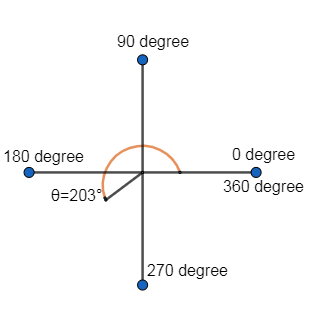
Therefore, for the given angle $\theta ={{203}^{\circ }}$ , its reference angle is equal to ${{23}^{\circ }}$ and the standard position of this angle lies in the third quadrant.

Note: While solving this problem, do mention all the steps properly to avoid confusion. Always remember that after drawing the graph, the angle must be lying in the third quadrant. You can also convert the angle into radian form, and then draw the graph, to get the required solution for the problem.