Question

How do you find the reference angle of, $\theta =-{{245}^{\circ }}$, and sketch the angle in standard position?

Answer 1

Hint: To answer our question, we will first understand the meaning of a reference angle. The reference angle of any angle is the smallest angle made by the terminal of this specific angle with the X-axis. The measure of the reference angle is always less than or equal to 90 degrees and it is always positive in calculation.

Complete step by step solution:
We have been asked to calculate the reference angle of a negative angle. To calculate the reference angle of a negative angle, we will first of all calculate its coterminal angle. This can be done by successively adding ${{360}^{\circ }}$ to the negative angle until we get the smallest positive angle.
Let the angle given to us be denoted by ‘$\theta $’. Then, its coterminal angle (${{\theta }_{ct}}$) will be given by:
$\begin{align}
  & \Rightarrow {{\theta }_{ct}}=-{{245}^{\circ }}+{{360}^{\circ }} \\
 & \therefore {{\theta }_{ct}}={{115}^{\circ }} \\
\end{align}$
Now, this angle lies in the second quadrant. And, the formula for calculating the reference angle of a second quadrant angle is:
$\Rightarrow {{\theta }_{ref}}={{180}^{\circ }}-{{\theta }_{0}}$
Here, the value of ‘${{\theta }_{0}}$’ is equal to ‘${{\theta }_{ct}}$’ which has been calculated above. Using the value of ‘${{\theta }_{ct}}$’ and putting it in the equation of reference angle, we get:
$\begin{align}
  & \Rightarrow {{\theta }_{ref}}={{180}^{\circ }}-{{115}^{\circ }} \\
 & \therefore {{\theta }_{ref}}={{65}^{\circ }} \\
\end{align}$
Hence, the reference angle for, $\theta =-{{245}^{\circ }}$, comes out to be ${{65}^{\circ }}$. This can be drawn in standard form as follows:

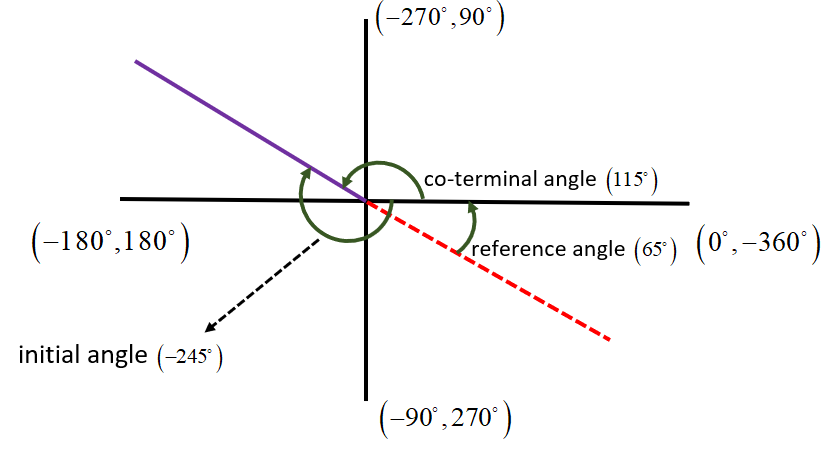
Hence, the reference angle has been calculated and sketched in a standard form.

Note:
If in our calculation, the reference angle comes out to be negative or greater than 90 degrees, then we should re-check our solution for any possible errors. This is a simple rule that can be used to verify our solution. Also, to save time in examination, one could use the direct formula for finding the reference angle of a negative angle. This formula is given by: $\Rightarrow {{\theta }_{ref}}=\min \left\{ \left| \theta -{{\left( 180n \right)}^{\circ }} \right|:n\in Z \right\}$.