Question

Find the ratio of tensions in the strings A and B if the system is in equilibrium.

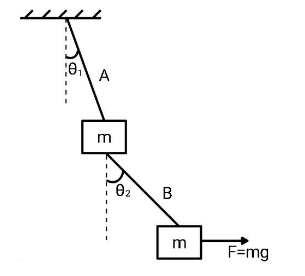
Answer 1

Hint: Here, you are given two blocks of mass $m$ which are connected to each other with the help of string B and the upper block is connected to string A which is attached to a ceiling. You are asked to find the ratio of tensions in both the strings, mathematically, you are asked to find $\dfrac{{{T_A}}}{{{T_B}}}$. In order to solve this question, you need to write the equations of motion using Newton’s laws of motion. After obtaining the equations, try to bring the term $\dfrac{{{T_A}}}{{{T_B}}}$ equal to some value and that value will be your answer.

Complete step by step answer:
The system is in equilibrium and so will be the upper block and lower block and hence the accelerations of both the blocks will be zero. The tension forces acting on each block are shown in the figure.

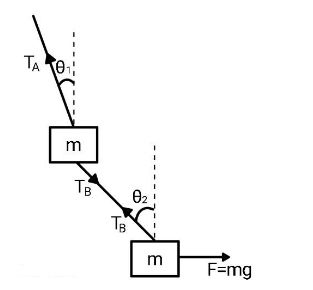
First, let us observe the upper block and write down the equation of motion for that block.
The forces acting on the upper block are:
(1) force due to gravity acting vertically downward,
(2) tension force due to string A acting along the string away from the block and
(3) tension force due to string B acting along the string away from the block.
For upper block, we have,
${T_A}\cos {\theta _1} - {T_B}\cos {\theta _2} - mg = 0...(1)$ and ${T_A}\sin {\theta _1} = {T_B}\sin {\theta _2}...(2)$

The forces acting on the lower block are:
(1) force due to gravity acting vertically downward,
(2) tension force due to string B acting along the string away from the block and
(3) applied force $F$ horizontally towards right.
For lower block, we have,
${T_B}\cos {\theta _2} = mg...(3)$ and ${T_B}\sin {\theta _2} = mg...(4)$.
From equation $3\& 4$, we get $\tan {\theta _2} = 1$, so we will have ${T_B} = \sqrt 2 mg$.
From equation $2$, we have $\dfrac{{{T_A}}}{{{T_B}}} = \dfrac{{\sin {\theta _2}}}{{\sin {\theta _1}}}$.

Divide equation $1$ by ${T_B}$, we get,
$\dfrac{{{T_A}}}{{{T_B}}}\cos {\theta _1} - \dfrac{{{T_B}}}{{{T_B}}}\cos {\theta _2} - \dfrac{{mg}}{{{T_B}}} = 0 \\
\Rightarrow\dfrac{{\sin {\theta _2}}}{{\sin {\theta _1}}}\cos {\theta _1} - \cos {\theta _2} - \dfrac{1}{{\sqrt 2 }} = 0 \\
\Rightarrow\dfrac{1}{{\sqrt 2 }}\dfrac{1}{{\tan {\theta _1}}} = \dfrac{2}{{\sqrt 2 }} \\
\Rightarrow\tan {\theta _1} = \dfrac{1}{2}..........(\sin {\theta _1} = \dfrac{1}{{\sqrt 5 }}\& \cos {\theta _1} = \dfrac{2}{{\sqrt 5 }} ) \\ $
In the above solution, we have used the result $\sin {\theta _2} = \cos {\theta _2} = \dfrac{1}{{\sqrt 2 }}$.
So, as we have $\dfrac{{{T_A}}}{{{T_B}}} = \dfrac{{\sin {\theta _2}}}{{\sin {\theta _1}}}$, we will have $\dfrac{{{T_A}}}{{{T_B}}} = \dfrac{{\dfrac{1}{{\sqrt 2 }}}}{{\dfrac{1}{{\sqrt 5 }}}} = \sqrt {\dfrac{5}{2}} $.

Therefore, the ratio of tensions in the strings A and B if the system is in equilibrium is $\sqrt {\dfrac{5}{2}}$.

Note:We have used Newton’s 2nd law of motion which states that the net force on a system is equal to mass times the acceleration of the system, as the acceleration of the system was zero in our case, the net force acting on each block will be zero, so keep this in mind. Also, observe and understand the way we obtained and substituted values of both the angles. You should always keep track of what values you obtain by solving equations.