Question

How do you find the ratio of surface area to volume in a rectangular prism?

Answer 1

Hint:We first try to define the concept of a rectangular prism where we formulate the volume of the prism as the multiplication of the dimensions of the prism. Then we find the surface area of the prism according to the surface area of a cuboid. Finally, we find the ratio of surface area to volume of that rectangular prism.

Complete step by step solution:
In case of rectangular prisms, the figure is more or less equal to the figure of a cuboid.

We first assume the dimensions of the prism which are $l,b,h$ for length, breadth and height
respectively.

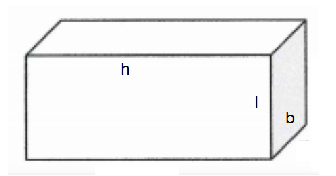
To find the surface area and volume we form the formulas according to the formulas of a cuboid.
So, we first find the surface area of the prism based on the opposite sides which are equal. The
the surface area of one plane is equal to the multiplication of two sides of that plane.

The different surface areas are $lb,bh,lh$ square units.

Therefore, the total surface area is $2\left( lb+bh+lh \right)$ square units.

The volume of the prism will be the multiplication of the dimensions of the prism.

Therefore, the total volume is $lbh$ cubic units.

Now we need to find the ratio of surface area to volume of that rectangular prism.

The ratio is $\dfrac{2\left( lb+bh+lh \right)}{lbh}$.

Note: We need to remember this formula of prism is only possible for regular prisms with particular bases. For other cases we have to apply the concept of differential and we need more given information on that to find the volume. The prism being regular, the sides of the prism are also rectangular.