Question

Find the ratio in which the line segment joining the points\[\left( { - 3,10} \right)\] and \[\left( {6, - 8} \right)\] is divided by \[\left( { - 1,6} \right)\].

Answer 1

Hint:For a better understanding we will make a line segment, and label the coordinates there and the assumptions on the segment itself. After that we will assume the ratio is \[k:1\] and the values of \[{m_1}{m_2}\] respectively. and after doing all this we will put it in the section formula.

Complete step by step answer:
For a better understanding we will make a line segment and allot the points on it,
A\[\left( { - 3,10} \right)\], B\[\left( {6, - 8} \right)\], C\[\left( { - 1,6} \right)\]

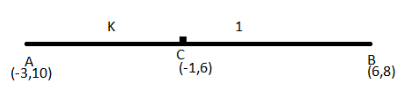
In the drawn diagram, we have to find the ratio between both the points $AC$ and $CB$. Let’s assume that the ratio is \[k:1\] so, \[{m_1} = k,{m_2} = 1\],
\[{x_1} = - 3,{x_2} = 6\]\[{y_1} = 10,{y_2} = - 8\]
Now using the section formula for further assessment, we get:
\[x = \left( {\dfrac{{{m_1}{x_2} + {m_2}{x_1}}}{{{m_1} + {m_2}}}} \right)\]
\[\Rightarrow - 1 = \left( {\dfrac{{k \times 6 + 1 \times - 3}}{{k + 1}}} \right) \\
\Rightarrow - 1 = \left( {\dfrac{{6k - 3}}{{k + 1}}} \right)\]
\[\Rightarrow - 1\left( {k + 1} \right) = 6k - 3\]
\[\Rightarrow - k - 1 = 6k - 3 \\
\Rightarrow - k - 6k = - 3 + 1 \\
\Rightarrow - 7k = - 2\]
\[\Rightarrow k = \left( {\dfrac{{ - 2}}{{ - 7}}} \right) \\
\Rightarrow k = \left( {\dfrac{2}{7}} \right)\]
Now we got the value of k and from our assumption its in ratio with 1.Hence the ratio is \[k:1\] so, now we can say that:
\[\dfrac{2}{7}:1\]
Multiplying 7 on both sides in order to equalise the ratio
\[7 \times \dfrac{2}{7}:7 \times 1 \Rightarrow 2:7\]
So, the ratio is \[2:7\].

Note:Above question can be solved easily. Generally, the students do not make diagrams and skip the labelling part which makes it quite difficult to visualise and hence one should always make a diagram for an easy solution.