
Find the ratio in which P(4, m) divides the line segment joining the points A(2, 3) and B(6, -3). Hence find m.
Answer
614.4k+ views
Hint: In this question to find the values of m, we will assume that the point P(4, m) divides the line joining the points A(2, 3) and B(6, -3) in the ratio of k : 1. And will use the section formula to find the value of m and k.
Complete step-by-step answer:
Now, we will use the section formula. The section formula tells us the coordinates of a point which divides a given line segment into two parts such that their lengths are in the ratio m: n. The Section formula to find a point (x, y) is
x = $\dfrac{{{\text{m}}{{\text{x}}_2}{\text{ + n}}{{\text{x}}_1}}}{{{\text{m + n}}}}$
y = $\dfrac{{{\text{m}}{{\text{y}}_2}{\text{ + n}}{{\text{y}}_1}}}{{{\text{m + n}}}}$
As we know A(2, 3) and B (6, -3) make a line segment AB. The line segment AB is divided at point P(4, m). So, we will apply section formula at point P.
Let P(4, m) divide the line segment AB in the ratio k : 1.
So, applying section formula at point P(4, m). We get,
x – coordinate of P = $\dfrac{{k\left( 6 \right) + 1\left( 2 \right)}}{{k + 1}}$ = $\dfrac{{6k + 2}}{{k + 1}}$
y – coordinate of P = $\dfrac{{k\left( { - 3} \right) + 1\left( 3 \right)}}{{k + 1}} = \dfrac{{ - 3k + 3}}{{k + 1}}$
Now as we know that the coordinates of point P is (4, m)
So, on comparing the x – coordinate of point P. We get,
$\dfrac{{6k + 2}}{{k + 1}} = 4$
Cross-multiplying above equation to find the value of k. We get,
4k + 4 = 6k + 2
Subtracting 4k + 2 to both the sides of the above equation. We get,
2k = 2
k = 1
Now to find the value of m we had to compare the y -coordinate of point P with m and put the value of k = 1.
So, m = $\dfrac{{ - 3k + 3}}{{k + 1}}$
Now putting the value of k as 1 in the RHS of the above equation. We get,
m = $\dfrac{{ - 3 + 3}}{{1 + 1}} = \dfrac{0}{2}$
Hence, the point P$\left( {4,0} \right)$ divides the line segment joining the points A(2, 3) and B(6, -3) in ratio 1 : 1.
So, P is the midpoint of line joining points A and B
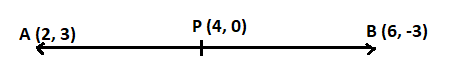
Note: While solving such types of questions, it is important to apply the section formula correctly. Most of the students made a mistake while applying the section formula. They replaced m from n and n from m. Also, apply the proper ratio for finding the coordinates of a point. Also, when only you have to find the value of a given variable, apply only that formula to find the value of the variable, for example if you are given that the x – coordinate of point is k, so you have to apply only the formula to find the x – coordinate of point.
Complete step-by-step answer:
Now, we will use the section formula. The section formula tells us the coordinates of a point which divides a given line segment into two parts such that their lengths are in the ratio m: n. The Section formula to find a point (x, y) is
x = $\dfrac{{{\text{m}}{{\text{x}}_2}{\text{ + n}}{{\text{x}}_1}}}{{{\text{m + n}}}}$
y = $\dfrac{{{\text{m}}{{\text{y}}_2}{\text{ + n}}{{\text{y}}_1}}}{{{\text{m + n}}}}$
As we know A(2, 3) and B (6, -3) make a line segment AB. The line segment AB is divided at point P(4, m). So, we will apply section formula at point P.
Let P(4, m) divide the line segment AB in the ratio k : 1.
So, applying section formula at point P(4, m). We get,
x – coordinate of P = $\dfrac{{k\left( 6 \right) + 1\left( 2 \right)}}{{k + 1}}$ = $\dfrac{{6k + 2}}{{k + 1}}$
y – coordinate of P = $\dfrac{{k\left( { - 3} \right) + 1\left( 3 \right)}}{{k + 1}} = \dfrac{{ - 3k + 3}}{{k + 1}}$
Now as we know that the coordinates of point P is (4, m)
So, on comparing the x – coordinate of point P. We get,
$\dfrac{{6k + 2}}{{k + 1}} = 4$
Cross-multiplying above equation to find the value of k. We get,
4k + 4 = 6k + 2
Subtracting 4k + 2 to both the sides of the above equation. We get,
2k = 2
k = 1
Now to find the value of m we had to compare the y -coordinate of point P with m and put the value of k = 1.
So, m = $\dfrac{{ - 3k + 3}}{{k + 1}}$
Now putting the value of k as 1 in the RHS of the above equation. We get,
m = $\dfrac{{ - 3 + 3}}{{1 + 1}} = \dfrac{0}{2}$
Hence, the point P$\left( {4,0} \right)$ divides the line segment joining the points A(2, 3) and B(6, -3) in ratio 1 : 1.
So, P is the midpoint of line joining points A and B
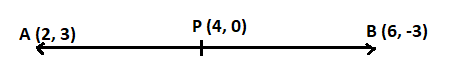
Note: While solving such types of questions, it is important to apply the section formula correctly. Most of the students made a mistake while applying the section formula. They replaced m from n and n from m. Also, apply the proper ratio for finding the coordinates of a point. Also, when only you have to find the value of a given variable, apply only that formula to find the value of the variable, for example if you are given that the x – coordinate of point is k, so you have to apply only the formula to find the x – coordinate of point.
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
What is the median of the first 10 natural numbers class 10 maths CBSE

Which women's tennis player has 24 Grand Slam singles titles?

Who is the Brand Ambassador of Incredible India?

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

A moving boat is observed from the top of a 150 m high class 10 maths CBSE




