Question

Find the range of the given function $ f\left( x \right)=\dfrac{1}{\sin x+1} $ ?

Answer 1

Hint: We start solving the problem by recalling the fact that the range of the function $ \sin x $ is $ \left[ -1,1 \right] $ . We then find the range of the function $ \sin x+1 $ . We then make use of fact that the minimum value of the function $ \dfrac{1}{h\left( x \right)} $ occurs at the maximum value of the function $ h\left( x \right) $ to find the minimum value of the function $ f\left( x \right) $ . We then make use of fact that the maximum value of the function $ \dfrac{1}{h\left( x \right)} $ occurs at the minimum value of the function $ h\left( x \right) $ to find the maximum value of the function $ f\left( x \right) $ . We then find the range by including all the values that lie in between these maximum and minimum values.

Complete step by step answer:
According to the problem, we are asked to find the range of the function $ f\left( x \right)=\dfrac{1}{\sin x+1} $ .
Now, let us assume $ f\left( x \right)=\dfrac{1}{\sin x+1}=\dfrac{1}{g\left( x \right)} $ .
We know that the range of the function $ \sin x $ is $ \left[ -1,1 \right] $ . So, we get the range of $ g\left( x \right)=\sin x+1 $ as $ \left[ 0,2 \right] $ ---(1).
We know that the minimum value of the function $ \dfrac{1}{h\left( x \right)} $ occurs at the maximum value of the function $ h\left( x \right) $ .
So, the minimum value of the function $ f\left( x \right) $ occurs at the maximum value of the function $ g\left( x \right) $ .
We have the maximum value of the function $ g\left( x \right) $ as 2 from equation (1). So, the minimum value of the function $ f\left( x \right) $ as $ \dfrac{1}{2} $ ---(2).
We know that the maximum value of the function $ \dfrac{1}{h\left( x \right)} $ occurs at the minimum value of the function $ h\left( x \right) $ .
So, the maximum value of the function $ f\left( x \right) $ occurs at the minimum value of the function $ g\left( x \right) $ .
We have the minimum value of the function $ g\left( x \right) $ as 0 from equation (1). So, the maximum value of the function $ f\left( x \right) $ as $ \dfrac{1}{0}=\infty $ ---(3).
Since the sine function is continuous, the function $ f\left( x \right) $ is also continuous. So, the range of the function $ f\left( x \right) $ is all the values that lie between maximum and minimum values which is $ \left[ \dfrac{1}{2},\infty \right) $ .

$ \therefore $ The range of the function $ f\left( x \right)=\dfrac{1}{\sin x+1} $ is $ \left[ \dfrac{1}{2},\infty \right) $ .

Note:
 We should not confuse Range with the domain while solving this type of problem. We can also solve this problem by plotting the given function as shown below:

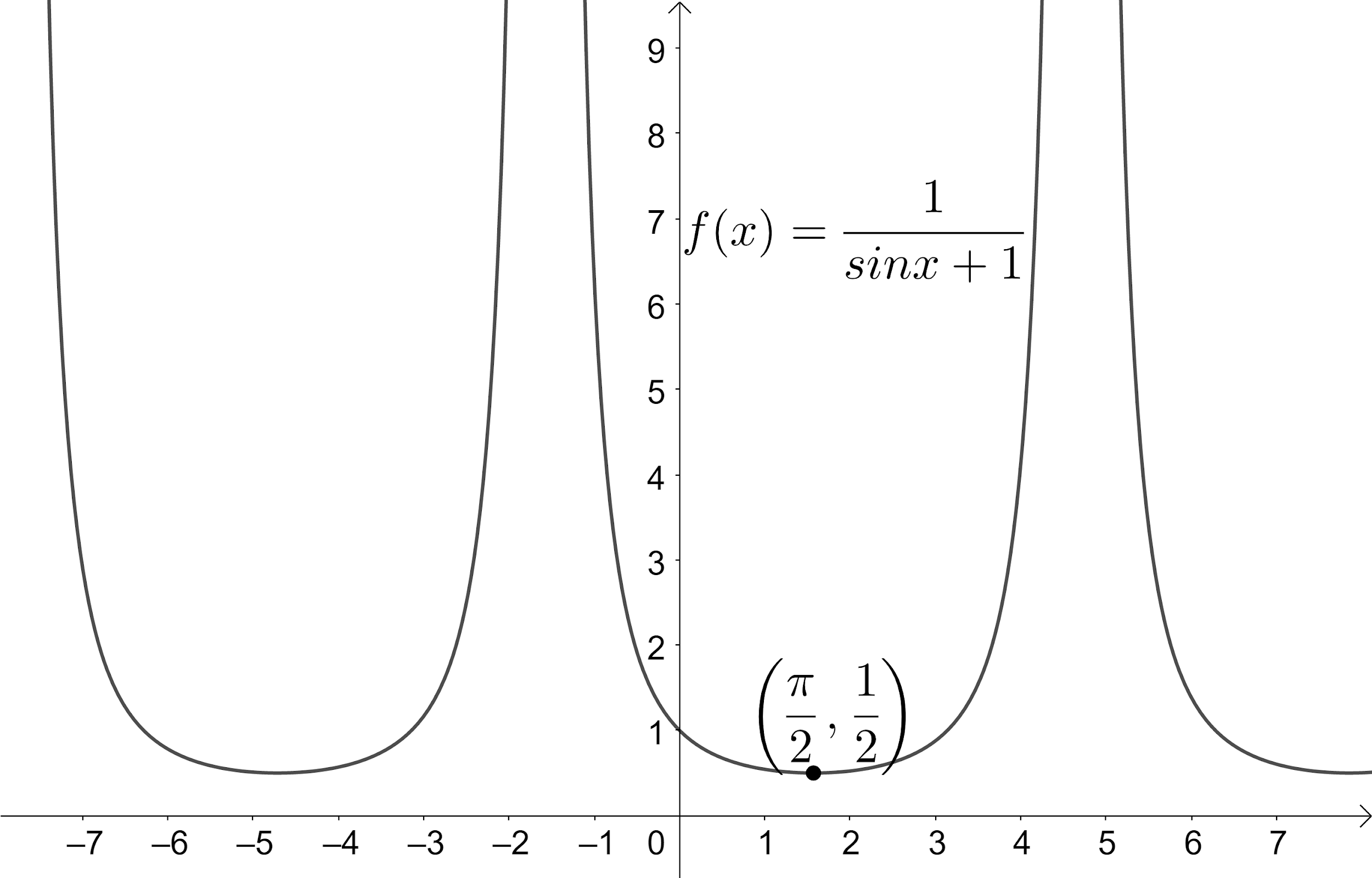
From the plot, we can see that the function has minimum value as $ \dfrac{1}{2} $ and maximum value as $ \infty $ which gives us the range of the function. Similarly, we can expect problems to find the domain of the given function $ f\left( x \right)=\dfrac{1}{\sin x+1} $ .