Question

Find the range of $ f(x) = \dfrac{{{x^2} + 34x - 71}}{{{x^2} + 2x - 7}} $ .

Answer 1

Hint: For this type of problem we first take f(x) as y then use this on cross-multiplying from a quadratic equation in terms of variable ‘x’ and as ‘x’ being domain of function ‘f’ being real. Then, equate discriminant of above formed quadratic equation greater than equal to zero to find required solution of the problem.

Complete step-by-step answer:
Given function is $ f(x) = \dfrac{{{x^2} + 34x - 71}}{{{x^2} + 2x - 7}} $
To find the range of the function we first take f(x) as y in the above equation. We have
 $ y = \dfrac{{{x^2} + 34x - 71}}{{{x^2} + 2x - 7}} $
Cross multiplying above equation.
 $
  y\left( {{x^2} + 2x - 7} \right) = {x^2} = + 34x - 71 \\
   \Rightarrow y{x^2} + 2xy - 7y = {x^2} + 34x - 71 \;
  $
Shifting terms to the left side and grouping to form a quadratic in terms of variable ‘x’.
 $
  y{x^2} + 2xy - 7y - {x^2} - 34x + 71 = 0 \\
   \Rightarrow \left( {y - 1} \right){x^2} + 2\left( {y - 17} \right)x + \left( {71 - 7y} \right) = 0 \;
 $
Since, x is the domain of a given function f(x). Therefore $ x \in R $ .
Hence, for all real values of ‘x’ we have discriminant of the above quadratic equation always greater than equal to zero.
 $
  D \geqslant 0 \\
  {b^2} - 4ac \geqslant 0 \;
  $
Substituting values from above formed quadratic equation we have
 $
  {\left\{ {2\left( {y - 17} \right)} \right\}^2} - 4\left( {y - 1} \right)\left( {71 - 7y} \right) \geqslant 0 \\
   \Rightarrow 4\left( {{y^2} + 289 - 34y} \right) - 4\left( {71y - 71 - 7{y^2} + 7y} \right) \geqslant 0 \\
   \Rightarrow {y^2} + 289 - 34y - 71y + 71 + 7{y^2} - 7y \geqslant 0 \\
   \Rightarrow 8{y^2} - 112y + 360 \geqslant 0 \\
   \Rightarrow {y^2} - 14y + 45 \geqslant 0 \;
  $
Making factors of above forms a quadratic equation by middle term splitting method.
 $
  {y^2} - 9y - 5y + 45 \geqslant 0 \\
   \Rightarrow y\left( {y - 9} \right) - 5\left( {y - 9} \right) \geqslant 0 \\
   \Rightarrow \left( {y - 9} \right)\left( {y - 5} \right) \geqslant 0 \;
  $
To find a set of solutions from above inequality we frame two cases.
Case I
Taking $ y - 9 \geqslant 0\,\,and\,\,y - 5 \geqslant 0 $
 $ \Rightarrow y \geqslant 9\,\,and\,\,y \geqslant 5 $

Therefore from above we see that feasible solution is $ [9,\infty ) $
Case II
 $
  y - 9 \leqslant 0\,\,and\,\,y - 5 \leqslant 0 \\
   \Rightarrow y \leqslant 9\,\,and\,\,y \leqslant 5 \;
  $
Therefore, from above we see that feasible solution is $ ( - \infty , - 9] $

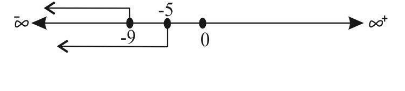
Hence, from above we see a feasible solution of the quadratic equation is $ ( - \infty ,9] $ U $ [9,\infty ) $ .
Therefore, range of the given function $ f(x) = \dfrac{{{x^2} + 34x - 71}}{{{x^2} + 2x - 7}} $ is $ ( - \infty , - 9] $ U $ [9,\infty ) $ .

Note: Whenever there is a problem of quadratic to quadratic first see if their factor are possible or if there is any common factor in both then first cancel common factors and then find range of the function, but if doing so is not possible then one can proceed with above method formula to get required solution of the problem.