Question

Find the range of $f\left( x \right)={{4}^{x}}+{{2}^{x}}+1$.
A. $\left( 0,\infty \right)$
B. $\left( 1,\infty \right)$
C. $\left( 2,\infty \right)$
D. $\left( 3,\infty \right)$

Answer 1

Hint: We first try to find the general term for the individual exponential forms. We try to find the minimum values for the exponential form when the base is positive. So, for any $a,a > 0$ we try to find the value of ${{a}^{x}} > 0,\forall x\in \mathbb{R}$. After getting the minimum part we try to understand the maximum value possible for the same function. We get the value the exponential terms tend to get. This way we find the range of the function.

Complete step by step answer:
We have a given function of exponential form $f\left( x \right)={{4}^{x}}+{{2}^{x}}+1$.
There are sum of two exponentials of positive numbers 2 and 4.
We know that for any $a,a>0$ we have ${{a}^{x}}>0,\forall x\in \mathbb{R}$.
We try to find the graphical representation of ${{a}^{x}}>0,\forall x\in \mathbb{R}$.

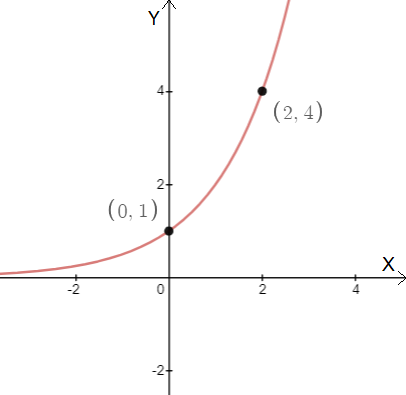
We see that the graph never goes under the X-axis for values of $a,a>0$.
So, replacing the value of a with both 2 and 4 we get ${{2}^{x}}>0$ and ${{4}^{x}}>0$.
Now, we place the minimum values of the terms in the function to find the minimum value of the whole function.
$f\left( x \right)={{4}^{x}}+{{2}^{x}}+1>0+0+1>1$.
The lower limiting value of the function is 1.
Now we need to find the maximum value. Again, the terms of ${{2}^{x}}$ and ${{4}^{x}}$ defines the maximum value of the function. The function is an increasing function.
If we take $g\left( x \right)={{a}^{x}}$ and the differentiation of the function $g\left( x \right)={{a}^{x}}$, we get
\[\begin{align}
  & g\left( x \right)={{a}^{x}} \\
 & \Rightarrow {{g}^{'}}\left( x \right)={{a}^{x}}\log a \\
\end{align}\]
The slope of the function is always positive as both \[{{a}^{x}}\] and \[\log a\] are positive.
The value of \[{{a}^{x}}\] keeps increasing towards $\infty $ as long we keep increasing the value of x.
This way we can say there is no maximum value of ${{2}^{x}}$ and ${{4}^{x}}$ as it tends to infinity.
Again, we place the maximum values of the terms in the function to find the minimum value of the whole function.
$f\left( x \right)={{4}^{x}}+{{2}^{x}}+1\to \infty +\infty +1\to \infty $.
The limiting value of the function is 1.
So, the range of the function $f\left( x \right)={{4}^{x}}+{{2}^{x}}+1$ is $\left( 1,\infty \right)$.

The correct option is B.

Note:
We need to place a point to get the idea how the exponential terms work. We mainly were trying to find the extremum values for its domain. The limit of the function is non-existent. This is not a converging sequence. The minimum value of the exponential is independent of x. it can never attain negative value. As x goes in negative for $x=-m,m>0$, we can say that ${{a}^{x}}={{a}^{-m}}=\dfrac{1}{{{a}^{m}}}$. The value still remains positive.