Question

Find the radius of the circle in which a central angle of \[{{60}^{\circ }}\]intercepts an arc of length 37.4 cm ( use \[\pi =\dfrac{22}{7}\])

Answer 1

Hint: To solve this type of problem first we have to convert the angle from degrees to radians. After converting use the formula to get the value of the radius. And get the value of radius in cm.

Complete step-by-step answer:

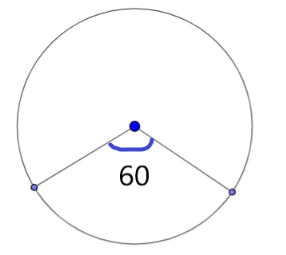
Given l = 37.4 cm and \[\theta ={{60}^{\circ }}\]
To convert degrees to radian we have to use
Radian measure = \[\dfrac{\pi }{180}\times \]Degree measure.
By entering the value of \[\theta ={{60}^{\circ }}\]in the above conversion we get,
\[=\dfrac{\pi }{180}\times 60\]
\[=\dfrac{60\pi }{180}\]
\[=\dfrac{\pi }{3}\] . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . (1)
We have to use the formula \[l=r\theta \] . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (2)
Where \[\theta \]is in radians.
Substituting the values of l and \[\theta \] in (2) we get
\[r=\dfrac{l}{\theta }\]
\[r=\dfrac{37.4}{\dfrac{\pi }{3}}\]
\[r=\dfrac{37.4}{\dfrac{22}{7\times 3}}\]
\[r=35.7cm\]
Therefore the radius is \[r=35.7cm\]
Note: This is a direct problem with the conversion of degrees to radians is the primary step. In the above formula \[\theta \] is in radians. Radius is measured in cm. Care should be taken while doing calculations.