Question

Find the radians, degrees, and grades the angle between the hour-hand and the minute-hand of a clock at (1) half past three.

Answer 1

Hint: To find the radians and degrees made by the hour-hand and the minute-hand of the clock at half past three first of all as we know that clock is in a shape of a circle and the total angle made by circle is ${360^\circ}$ and in one complete revolution total number of hours made by the clock is 12 hours. So, we can say that in 12 hours = ${360^\circ}$
We can understand it with the help of the diagram given below:

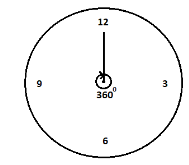
Now, we can find the angle made by the hour-hand in 1 hour, same as we can find the angle made by the hand-hour of the clock in 3 hours and 30 minutes. Now, we have to find the angle covered by the minute-hand. As we know angles are made in 1 hour $ = {30^\circ}$ and there are 60 minutes in 1 hour, so we can find the angle made by the minute-hand in 1 minute. We can understand it with the help of the diagram given below:

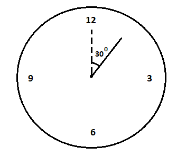
Now, we can find the angle made between the hour-hand and the minute-hand of a clock at half past three by subtracting the angle made by the hour-hand and minute-hand of the clock at half past three. To convert the degree into radians we can use the formula given below,

Formula used: Angle in radian $ = \theta \times \dfrac{\pi }{{{{180}^\circ}}}$…………………………(a)

Complete step-by-step answer:
Step 1: First of all to find the angle between hour-hand and the minute-hand of a clock at (1) half past three we have to find how much time has been spent. Hence, according to the (1) part given in the question time is half past three means 30 minutes past 3’Oclock so, we can say that the given time is: 3:30.
Step 2: As we know that the total angle made by a circle ${360^\circ}$ and the clock is also in the form of a circle. As we know the number of hours made by a clock in its complete revolution is 12hours. So, we can say that the angle made by a clock in 12 hours is ${360^\circ}$.
12 hours = ${360^\circ}$
Step 3: Now, as we know 12 hours = ${360^\circ}$ so we can find the angle made by the clock in 1 hour.
Angle made by the clock in 12 hours = ${360^\circ}$
Angle made by the clock in 1 hour$ = \dfrac{{{{360}^\circ}}}{{12}}$
Hence,
Angle made by the clock in 1 hour$ = {30^\circ}$
Step 4: As we have obtained, 1 hour$ = {30^\circ}$ and In 1 hour = 60minutes.
Hence,
60 minutes $ = {30^\circ}$
Step 5: As we know, 60 minutes $ = {30^\circ}$ so,
Angle made in 1 minute$ = \dfrac{{{{60}^\circ}}}{{30}}$
1 minute$ = {\dfrac{1}{2}^\circ}$
Step 6: As the time given the (1) part of the question is 3:30 means hour-hand has to cover 3 hour and 30 minutes from 12’Oclock to 3:30.
3 hours + 30 minutes = (3$ \times $1 hour) + (30 $ \times $1 minute)
From the steps (3, and 5) we have obtained that, angle made by the clock in 1 hour$ = {30^\circ}$ and the angle made in 1 minute$ = {\dfrac{1}{2}^\circ}$
Hence, the total angle made by the hour-hand of the clock is:
$
   = 3 \times {30^\circ} + 30 \times {\dfrac{1}{2}^\circ} \\
   = {90^\circ} + {15^\circ} \\
   = {105^\circ}...............................(1) \\
 $
Step 7: similarly now, we have to find the angle made by the minute hand of the clock.
As we know that, 60 minutes $ = {360^\circ}$ hence,
Angle made by the clock in 60 minutes $ = {360^\circ}$
Angle made by the clock in 1 minute$ = \dfrac{{{{360}^\circ}}}{{60}}$
 Angle made by the clock in 1 minute$ = {6^\circ}$
Step 8: From the step 7 as we know that Angle made by the clock in 1 minute$ = {6^\circ}$ hence, the angle cover by the minute-hand of the clock in 30 minutes is:
$ = 30 \times {6^\circ}$
Angle made by the minute-hand in 30 minutes$ = {180^\circ}$……………………………..(2)
Step 9: Now, we can find the angle made between the hour-hand and the minute-hand of a clock at half past three is by subtracting equation (1) from equation (2)
Hence,
Angle between the hour-hand and the minute-hand at 3:30$ = {180^\circ} - {105^\circ}$
Angle between the hour-hand and the minute-hand at 3:30$ = {75^\circ}$
We can understand it with the help of the diagram given below:

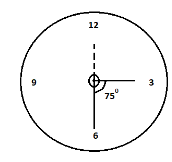
Step 10: As we have obtained the angle in degree now we can find the angle made by hour-hand and the minute-hand for 3:30 minutes in radians. Now, to convert the degree into radians we will use the formula (a) as mentioned in the solution hint.
On substituting the value of $\theta $ in formula (a),
Angle in radians$ = {75^\circ} \times \dfrac{\pi }{{{{180}^\circ}}}$
On solving,
Angle of radians$ = \dfrac{{5\pi }}{{12}}$

Hence, Angle made by the hour-hand and the minute-hand at 3:30minutes in radians $ = \dfrac{{5\pi }}{{12}}$

Note: As we all know that a clock is in the shape of a circle and the total angle made by the circle is ${360^\circ}$ so with the help of this angle we can find the angle required.
There are 12 hours shown in a clock and there are 60 minutes in 1 hour.
To find the angle covered by the hour-hand and minute-hand we will have to consider from 12’Oclcok.