Question

How do you find the quadratic function $y = f(x)$ whose graph has a vertex $( - 4,{\kern 1pt} {\kern 1pt} {\kern 1pt} 4)$ and passes through the point $( - 8,{\kern 1pt} {\kern 1pt} {\kern 1pt} 0)$?

Answer 1

Hint: The general form of a quadratic function is given as $f(x) = a{x^2} + bx + c$. The graph of a quadratic function is parabolic. We can write this function in vertex form as $(y - k) = a{(x - h)^2}$, where $(h,{\kern 1pt} {\kern 1pt} {\kern 1pt} k)$ is the vertex and $a \ne 0$. To find the function we have to find the value of $a$.

Complete step by step solution:
We have to find a quadratic function, which we know will be parabolic. We can write the general form of the quadratic function as $f(x) = a{x^2} + bx + c$. We can also write the same quadratic function in vertex form as,
$(y - k) = a{(x - h)^2}$
where $(h,{\kern 1pt} {\kern 1pt} {\kern 1pt} k)$ is the vertex and $a$ is any constant number.
From the information given in the question, vertex of the function is $( - 4,{\kern 1pt} {\kern 1pt} {\kern 1pt} 4)$.
Therefore, $h = - 4$ and $k = 4$.
Thus, putting the values of $h = - 4$ and $k = 4$, we get the function as
$
  (y - 4) = a{(x + 4)^2} \\
   \Rightarrow y = a{(x + 4)^2} + 4 \\
 $
Now we have to find the value of $a$.
We are also given that the function passes through the point $( - 8,{\kern 1pt} {\kern 1pt} {\kern 1pt} 0)$. So this point should satisfy the required function. So we can write,
$
  y = a{(x + 4)^2} + 4 \\
   \Rightarrow 0 = a{( - 8 + 4)^2} + 4 \\
   \Rightarrow 0 = a{( - 4)^2} + 4 \\
   \Rightarrow 0 = 16a + 4 \\
   \Rightarrow 16a = - 4 \\
   \Rightarrow a = \dfrac{{ - 4}}{{16}} = \dfrac{{ - 1}}{4} \\
 $
So we get the value of $a = \dfrac{{ - 1}}{4}$
Putting this in the function, we get,
$y = - \dfrac{1}{4}{(x + 4)^2} + 4$
This is the function in the vertex form. We can transform it into general form as,
\[
  y = - \dfrac{1}{4}{(x + 4)^2} + 4 \\
   \Rightarrow y = - \dfrac{1}{4}({x^2} + 8x + 16) + 4 \\
   \Rightarrow y = - \dfrac{1}{4}{x^2} - 2x - 4 + 4 \\
   \Rightarrow y = - \dfrac{{{x^2}}}{4} - 2x \\
 \]
Hence, the required function is \[y = f(x) = - \dfrac{{{x^2}}}{4} - 2x\]
The graph of the above function is as shown below,

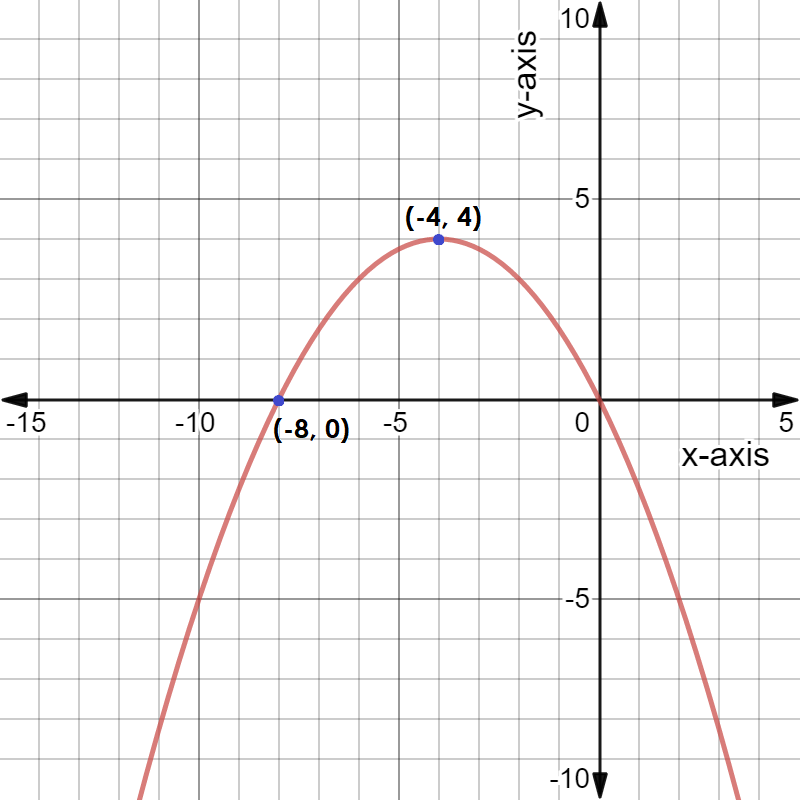
Note: We can see in the graph that the curve is parabolic with vertex at $( - 4,{\kern 1pt} {\kern 1pt} {\kern 1pt} 4)$ and passes through the point $( - 8,{\kern 1pt} {\kern 1pt} {\kern 1pt} 0)$. We got a negative value of $a$ so the parabola has its mouth open towards negative y-axis. The vertex is the point in the parabola where the function takes the maximum value in this case.