Question

How do you find the quadratic function whose graph has a vertex of $\left( 4,5 \right)$ and passes through the given point of $\left( 6,17 \right)$?

Answer 1

Hint: We will look at the general equation for the vertex form of a quadratic equation. We will see the components of this equation and what is being represented by them. Then we will form a quadratic equation in its vertex form using the general equation and the given vertex. Then we will use the point through which the parabola passes to obtain the missing value of the vertex form quadratic equation.

Complete step by step answer:
We know that the graph of a quadratic equation is always a parabola. Now, we know that the general quadratic equation is given by $f\left( x \right)=a{{x}^{2}}+bx+c$. Now, we will look at the vertex form of the quadratic equation. The vertex form of the quadratic equation is given by
$f\left( x \right)=a{{\left( x-h \right)}^{2}}+k$
where $a\ne 0$ and $\left( h,k \right)$ is the vertex. This vertex is the vertex of the parabola that represents the graph of the quadratic equation. Using this vertex form of the quadratic equation, we can determine the vertex of the parabola and the direction in which the parabola is facing. If $a$ is positive, then the parabola is facing upwards and if $a$ is negative, then the parabola is facing downwards.
Now, we are given that the vertex is $\left( 4,5 \right)$. So, substituting the coordinates of the vertex in place of $\left( h,k \right)$ in the general equation in vertex form, we get the following,
$f\left( x \right)=a{{\left( x-4 \right)}^{2}}+5....(i)$
Next, we know that the graph passes through the point of $\left( 6,17 \right)$. Also, $y=f\left( x \right)$. Therefore, we will substitute $x=6$ and $y=17$ in the above equation. We get the following equation,
$17=a{{\left( 6-4 \right)}^{2}}+5$
Solving this equation for $a$, we get
$\begin{align}
  & 17=a{{\left( 2 \right)}^{2}}+5 \\
 & \Rightarrow 17-5=4a \\
 & \Rightarrow 4a=12 \\
 & \therefore a=3 \\
\end{align}$
Now, we will substitute $a=3$ in equation $(i)$ in the following manner,
$\begin{align}
  & f\left( x \right)=3{{\left( x-4 \right)}^{2}}+5 \\
 & \Rightarrow f\left( x \right)=3\left( {{x}^{2}}-8x+16 \right)+5 \\
 & \Rightarrow f\left( x \right)=3{{x}^{2}}-24x+48+5 \\
 & \therefore f\left( x \right)=3{{x}^{2}}-24x+53 \\
\end{align}$

The quadratic equation we obtained is $f\left( x \right)=3{{x}^{2}}-24x+53$. The graph of this equation looks like the following,

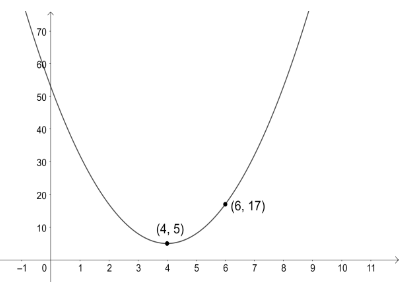
Note: We obtained $a=3$, which is positive. Therefore, the parabola represented by the quadratic equation obtained faces upwards. We used the algebraic identity ${{\left( a+b \right)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}$ in the calculations. It is useful to know such identities as they make the calculations easier. It is important to do the calculations explicitly so that minor mistakes can be avoided.