Question

Find the quadrant or axis in/on which the following point lies $$\left(-5,7\right)$$?
A. I
B. II
C. III
D. None of these

Answer 1

Hint: Here, we are given a point and we need to find out in which quadrant it lies. Also, one should note that the x coordinate is always written first and the y coordinate is written next. And so, starting from the top right corner is Quadrant I and then, in a counter clockwise direction you will see Quadrants II, III and IV. Thus, we will notice the sign of the coordinates in each point and then compare them with the standard form of the quadrants to get the final output.

Complete step by step answer:
Given, one point $$\left(-5,7\right)$$
We know that, when we draw a horizontal line and then a vertical line, both intersect and that intersection point is called the origin. Then, from the reference of origin and those two lines we define quadrants, the horizontal line is called x-axis and the vertical line is called y-axis and so we get 4 quadrants in all.
For this, we will first understand the type of points every quadrant has and then compare them with the given point to find the required quadrant in which the given point lies.
So, we have drawn the figure below:

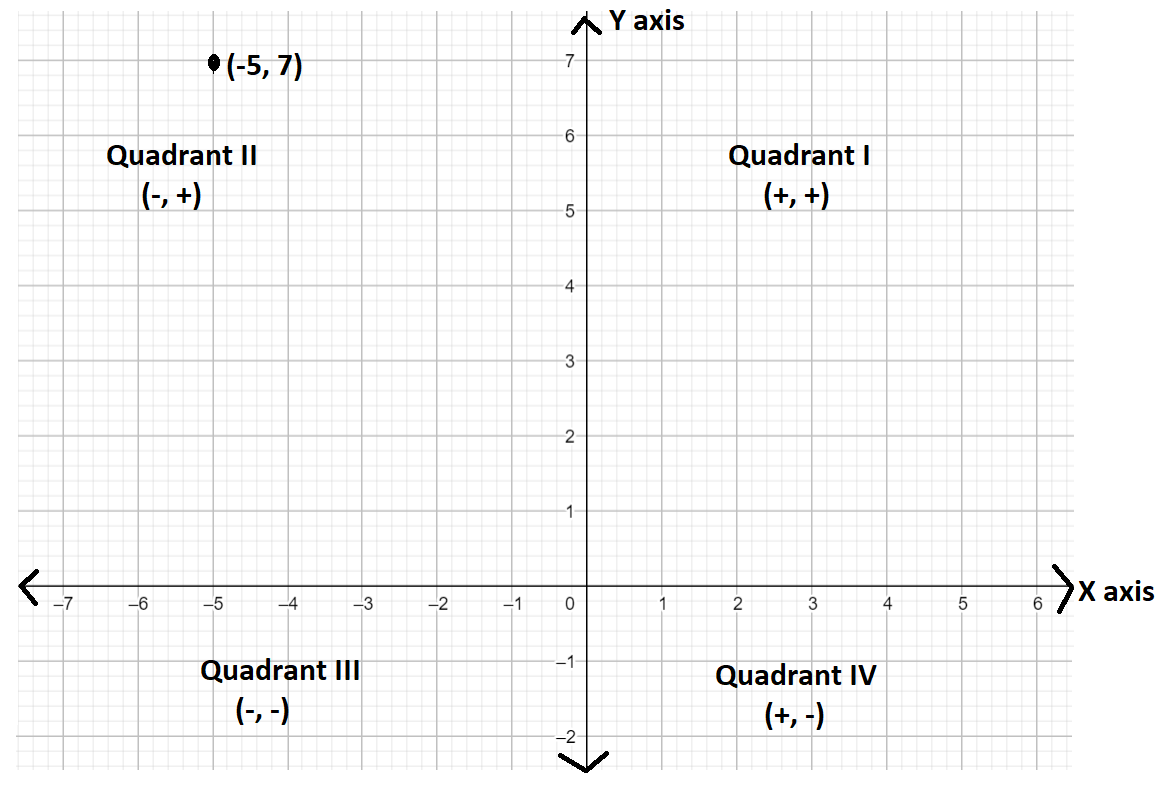
According to the figure, both the coordinates are there in all the 4 quadrants as shown below:
1) 1st quadrant: x is positive and y is positive
2) 2nd quadrant: x is negative and y is positive
3) 3rd quadrant: x is negative and y is negative
4) 4th quadrant: x is positive and y is negative.
We are given a point $$\left(-5,7\right)$$ and in this, x is negative and y is positive.
So, from the figure, we can say that this point is in the 2nd quadrant.

Hence, the point $$\left(-5,7\right)$$ lies in quadrant II.

Note:
A quadrant is the area contained by the x and y axis. To explain this, the two dimensional Cartesian plane is divided by the x and y axis into four quadrants. Students often make mistakes in naming quadrants in the Cartesian plane. Also remember, the quadrant starts from the top right corner and moves in an anticlockwise direction.