Question

Find the principal value of \[{\sec ^{ - 1}}( - 2)\].

Answer 1

Hint: In the given question, we have to apply trigonometric identities and rules of principal value to solve the question. If the equation involves a variable \[0 \leqslant x \leqslant 2\pi \], then the solutions are called principal solutions.

Complete step by step solution:
In order to find the value of \[{\sec ^{ - 1}}x\], we can follow the following steps:
Let \[\sec \theta = x(\left| x \right| \geqslant 1,x \geqslant 1,x \leqslant - 1)\] then we will get:
\[\theta = \sec - 1x\]
Here \[\theta \] has infinitely many values.
Let \[0 \leqslant \alpha \leqslant \pi \] where:
\[\alpha \] is \[(\alpha \ne \dfrac{\pi }{2})\] non-negative smallest numerical value of these infinite number of values and satisfies the equation \[\sec \theta = x\] then the angle \[\alpha \] is called the principal value of \[{\sec ^{ - 1}}x\].
Now let us solve the sum as follows:
Let \[x = {\sec ^{ - 1}}( - 2)\]
Using the property \[{\sec ^{ - 1}}A = B\] so \[\sec B = A\], we will get:
\[ \Rightarrow \sec x = - 2\]
Using the trigonometric ratio table, we will get \[\sec \dfrac{\pi }{3} = 2\]. Thus, we will get:
\[ \Rightarrow \sec x = - \sec \dfrac{\pi }{3}\]
Again, using the trigonometric ratio table, we will get \[\operatorname{Sec} ( - 1) = \pi \] so we can conclude that:
\[ \Rightarrow \sec x = \sec (\pi - \dfrac{\pi }{3})\]
Equalizing the denominator on the RHS, we get,
\[ \Rightarrow \sec x = \sec (\dfrac{{2\pi }}{3})\]
Hence, we can get the value\[x\] of as follows:
\[ \Rightarrow x = \dfrac{{2\pi }}{3}\]
Since we have assumed \[x = {\sec ^{ - 1}}( - 2)\], substituting the value, we will get,
\[ \Rightarrow {\sec ^{ - 1}}( - 2) = \dfrac{{2\pi }}{3}\]
Thus, the principal value of \[{\sec ^{ - 1}}( - 2)\] will be \[\dfrac{{2\pi }}{3}\].
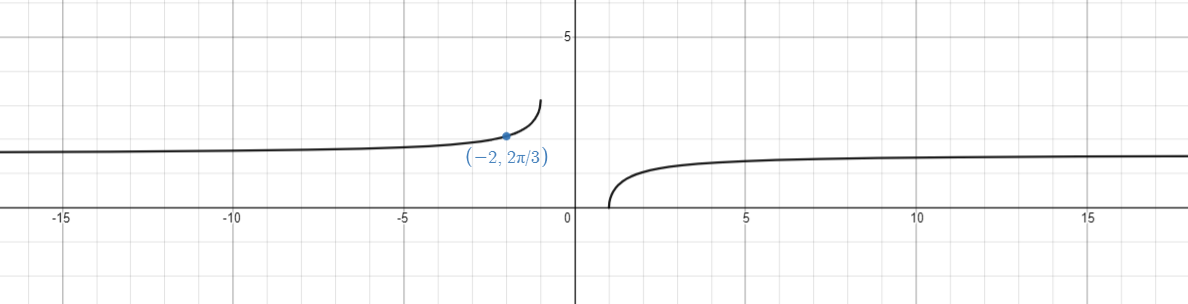
The following graph shows the principal value of \[{\sec ^{ - 1}}( - 2)\].

Note:
1) If the principal value of \[{\sec ^{ - 1}}x\] is \[\alpha \], \[(0 < \alpha < \pi )\] and \[(\alpha \ne \dfrac{\pi }{2})\] then its general value = \[2n\pi \pm \alpha \], where, \[\left| x \right| \geqslant 1\].
Therefore, \[{\sec ^{ - 1}}x = 2n\pi \pm \alpha \], where, \[(0 \leqslant \alpha \leqslant \pi )\], \[\left| x \right| \geqslant 1\] and \[\alpha \ne \dfrac{\pi }{2}\].
In the given sum, the general value of \[{\sec ^{ - 1}}( - 2)\] will be \[2n\pi \pm \dfrac{{2\pi }}{3}\]after solving the principal value.
2) \[{\sec ^{ - 1}}A = B\] is simplified by simple cross multiplication as follows:
\[{\sec ^{ - 1}}A = B\] can be rewritten as-
\[\dfrac{1}{{\sec }}A = B\]
Cross-multiplying on the other side, we will get,
\[A = \sec B\]
3) When there are two values, one is positive and the other is negative such that they are numerically equal, then the principal value is the positive one. For example, \[{\sin ^{ - 1}}(x)\]with domain \[( - 1,1)\] will have range of \[( - \dfrac{\pi }{2},\dfrac{\pi }{2})\].