Question

Find the potential difference between the points \[A\] and \[B\] and that between \[E\] and \[F\] of the circuit shown in the figure:

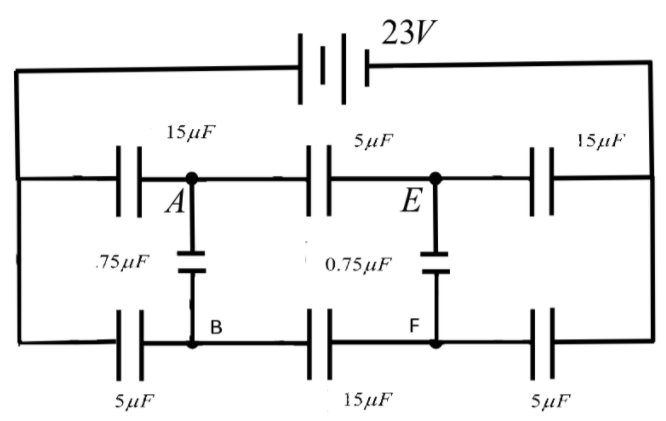
Answer 1

Hint: To find the potential differences between \[A\] and \[B\] and \[E\] and \[F\], we consider distribution of charges through each branch according to junction rule. Then we will apply the loop rule in different loops and then find the charges passing through each branch. Then we will use the equation for capacitance to determine the potential difference across the desired points.

Complete step-by-step solution:
Firstly we will assign the distribution of charge through every branch according to the junction rule which states current entering will be equal to current leaving from a junction in a circuit. We will assign them and take 3 loops as shown in the figure.

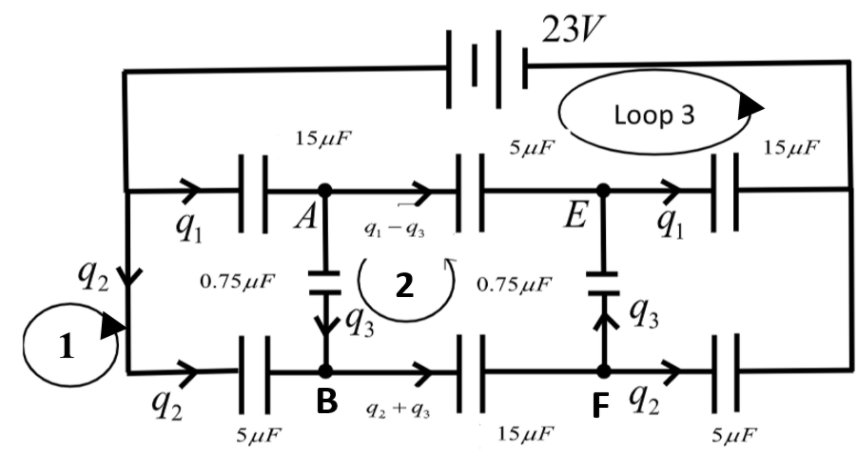
Now, we will apply KVL in each of the loop taken and form expressions for charges \[{{q}_{1}},{{q}_{2}}\] and \[{{q}_{3}}\].
When we apply KVL for the first loop, we will get
      \[-\dfrac{{{q}_{2}}}{5}+\dfrac{{{q}_{3}}}{0.75}+\dfrac{{{q}_{1}}}{15}=0\]
      \[\Rightarrow {{q}_{1}}-3{{q}_{2}}+20{{q}_{3}}=0\] --- (1)
Now we will apply KVL for the second loop,
\[-\dfrac{{{q}_{2}}+{{q}_{3}}}{15}-\dfrac{{{q}_{3}}}{0.75}+\dfrac{{{q}_{1}}-{{q}_{3}}}{5}-\dfrac{{{q}_{3}}}{0.75}=0\]
      \[\Rightarrow 3{{q}_{1}}-{{q}_{2}}+44{{q}_{3}}=0\] --- (2)
Then for third loop,
   \[23-\dfrac{{{q}_{2}}}{5}-\dfrac{{{q}_{2}}+{{q}_{3}}}{15}-\dfrac{{{q}_{2}}}{5}=0\]
      \[\Rightarrow 345=7{{q}_{2}}+{{q}_{3}}\] --- (3)
Now we will solve for \[{{q}_{1}},{{q}_{2}}\] and \[{{q}_{3}}\] by equating the obtained expressions.
\[(2)\times (3)-(1)\Rightarrow 9{{q}_{1}}-3{{q}_{2}}-44\times 3{{q}_{3}}=0\]
   \[\begin{align}
  & 8{{q}_{1}}=152{{q}_{3}} \\
 & \Rightarrow {{q}_{1}}=19{{q}_{3}} \\
\end{align}\]
    Substitute this in (3),
  \[\begin{align}
  & 345=95{{q}_{3}}-{{q}_{3}} \\
 & \Rightarrow {{q}_{3}}=\dfrac{345}{92} \\
\end{align}\]
Now, we will find other charges as,
\[\Rightarrow {{q}_{1}}=\dfrac{19\times 345}{92}\]
\[\Rightarrow {{q}_{2}}=\dfrac{13\times 345}{92}\]
So we have found all the charges. Now, we will find the potential difference from the expression from expression given for finding capacitance. i.e. \[C=\dfrac{q}{V}\].
For potential difference between \[AB\],
 \[{{V}_{AB}}=\dfrac{q}{C}\]
\[\Rightarrow {{V}_{AB}}=\dfrac{{{q}_{3}}}{C}=\dfrac{345}{92\times 0.75\mu F}=5V\].
Therefore, \[{{V}_{AB}}=5V\].
Through branch \[EF\], the same charge is flowing and capacitance is the same. That is \[{{V}_{EF}}=5V\].
So the potential difference through both branches is \[5V\].

Note: We must be aware of the usage of junction rule and loop rule properly and only take the loops which are needed. This question can also be solved by finding the total capacitance of the whole circuit and finding the charge stored at each capacitor. After finding the charge, divide it by the capacitance of the given capacitor to find the drop of potential on that capacitor. Hence the potential difference.