Question

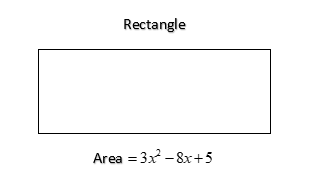
Find the possible expressions for the length and breadth of the rectangle whose area is $3{x^2} - 8x + 5$ ?

Answer 1

Hint- In this type of question since we know that the area of the rectangle is equal to length multiplied by breadth. So, we will just approach this problem in such a way that we will just factorize the polynomial into two factors such that it resembles the formula for the Area of rectangle $ = length \times breadth$ and we will factorize the polynomial on the basis of middle term splitting.

Complete step-by-step answer:
Given area of the rectangle $ = 3{x^2} - 8x + 5$

We will use the middle term splitting
we will find the product of the first and the last term which is 3 and 5 and the product is $3 \times 5 = 15$.
Now, find the factors of 15 such that addition or subtraction of those factors results in the middle term which is -8.
The two factors come up to be -3 and -5 as on their multiplication we get 15 and, on their addition, we get -8.
Now, rewrite the polynomial like, $3{x^2} - 3x - 5x + 5$ . Now, regroup the terms by finding the common factors like here we get the polynomial as $3x(x - 1) - 5(x - 1)$ by taking 3$x$ common from the first two terms and -5 common from the last two terms.
Now, factor out the shared binomial parenthesis i.e. $(x - 1)$
$(3x - 5)(x - 1)$
Now, it’s been split up into two factors which is resembling the formula for area of rectangle $ = length \times breadth$
So, possible expressions for the length and breadth are $3x - 5,x - 1$
Hence, the possible expressions for the length and breadth of the rectangle whose area is $3{x^2} - 8x + 5$ are $3x - 5,x - 1$ .

Note- For such questions, just relate the given expression of area to the formula for the area of rectangle where area of rectangle $ = length \times breadth$ due to which we get the possible expressions for the length and breadth of the rectangle by the concept of factoring a quadratic polynomial on the basis of any of the techniques we want to.