Question

Find the position vectors of a point R which divides the line joining two points P and Q whose position vectors are \[2\overrightarrow{a}+\overrightarrow{b}\] and \[\overrightarrow{a}-3\overrightarrow{b}\] respectively, externally in the ratio 1:2. Also, show that P is the midpoint of the line segment RQ.

Answer 1

Hint:First of all, draw a line segment PQ in which R is dividing externally in the ratio 1:2. Now use the formula, \[\dfrac{{{m}_{1}}\left( {{P}_{2}} \right)-{{m}_{2}}\left( {{P}_{1}} \right)}{{{m}_{1}}-{{m}_{2}}}\] to find the position vector of R where ${m}_1$ and ${{m}_2}$ are ratio which R divides externally. Now, find the midpoint of RQ by using the formula, \[\dfrac{{{P}_{1}}+{{P}_{2}}}{2}\] and verify the given result.

Complete step-by-step answer:
Here, we are given that the position vectors of a point R which divides the line joining two points P and Q whose position vectors are \[2\overrightarrow{a}+\overrightarrow{b}\] and \[\overrightarrow{a}-3\overrightarrow{b}\] respectively, externally in the ratio 1:2. We have to find the position vector of point R. Also, we have to show that P is the midpoint of the line segment RQ.
Let us first draw the line segment PQ such that R divides it externally in the ratio 1:2.

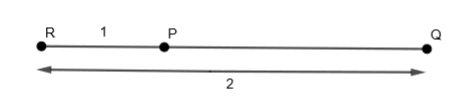
Here, we are given that position vectors of P and Q are \[2\overrightarrow{a}+\overrightarrow{b}\] and \[\overrightarrow{a}-3\overrightarrow{b}\] respectively. We know that the position vector of any point A is given by \[\overrightarrow{OA}\]. So, we get,
\[\overrightarrow{OP}=2\overrightarrow{a}+\overrightarrow{b}\]
\[\overrightarrow{OQ}=\overrightarrow{a}-3\overrightarrow{b}\]
We know that when any point (say A) divides a line segment externally. So, its position vector is given by the sectional formula as,
\[\overrightarrow{OA}=\dfrac{{{m}_{1}}\left( {{P}_{2}} \right)-{{m}_{2}}\left( {{P}_{1}} \right)}{{{m}_{1}}-{{m}_{2}}}\]
From the diagram, we can see that \[{{m}_{1}}=1,{{m}_{2}}=2,{{P}_{1}}=\overrightarrow{OP}=2\overrightarrow{a}+\overrightarrow{b}\] and \[{{P}_{2}}=\overrightarrow{OQ}=\overrightarrow{a}-3\overrightarrow{b}\]
So, we get,
\[\overrightarrow{OR}=\dfrac{{{m}_{1}}\left( \overrightarrow{OQ} \right)-{{m}_{2}}\left( \overrightarrow{OP} \right)}{{{m}_{1}}-{{m}_{2}}}\]
\[=\dfrac{1\left( \overrightarrow{a}-3\overrightarrow{b} \right)-2\left( 2\overrightarrow{a}+\overrightarrow{b} \right)}{1-2}\]
\[=\dfrac{\overrightarrow{a}-3\overrightarrow{b}-4\overrightarrow{a}-2\overrightarrow{b}}{-1}\]
\[=\dfrac{-3\overrightarrow{a}-5\overrightarrow{b}}{-1}\]
\[=3\overrightarrow{a}+5\overrightarrow{b}\]
So, we get the position vector of R as \[3\overrightarrow{a}+5\overrightarrow{b}\].
Now, let us find the midpoint of RQ.

We know that the position vector of the midpoint (say A) of any line segment is given by:
\[\overrightarrow{OA}=\dfrac{\overrightarrow{{{P}_{1}}}+\overrightarrow{{{P}_{2}}}}{2}\]
Here, from the above diagram, we can see that,
\[\overrightarrow{{{P}_{1}}}=\overrightarrow{OR}=3\overrightarrow{a}+5\overrightarrow{b}\]
\[\overrightarrow{{{P}_{2}}}=\overrightarrow{OQ}=\overrightarrow{a}-3\overrightarrow{b}\]
So, we get,
\[\overrightarrow{OM}=\dfrac{\overrightarrow{OR}+\overrightarrow{OQ}}{2}\]
\[\overrightarrow{OM}=\dfrac{3\overrightarrow{a}+5\overrightarrow{b}+\overrightarrow{a}-3\overrightarrow{b}}{2}\]
\[\overrightarrow{OM}=\dfrac{4\overrightarrow{a}+2\overrightarrow{b}}{2}\]
\[\overrightarrow{OM}=2\overrightarrow{a}+\overrightarrow{b}\]
This is equal to the position vector of P that is \[\overrightarrow{OP}=2\overrightarrow{a}+\overrightarrow{b}\].
So, we have proved that the midpoint of the line segment RQ is point P.

Note: In these types of questions, students often make mistakes while applying sectional formula by taking the wrong values of \[{{P}_{1}}\] and \[{{P}_{2}}\] or reversing their value. So, this must be taken care of. Also, take special notice, whether that point is dividing the line externally or internally. For external division use, \[\dfrac{{{m}_{1}}\left( {{P}_{2}} \right)-{{m}_{2}}\left( {{P}_{1}} \right)}{{{m}_{1}}-{{m}_{2}}}\] while for internal division, use \[\dfrac{{{m}_{1}}\left( {{P}_{2}} \right)+{{m}_{2}}\left( {{P}_{1}} \right)}{{{m}_{1}}+{{m}_{2}}}\].