Question

Find the point on the ellipse $4{{x}^{2}}+9{{y}^{2}}=1$ at which tangent is parallel to the line $8x=9y$.

Answer 1

Hint: In this question we have been given the equation of the ellipse and we have to find the point at which tangent is parallel to a line. We will first find out the slope of the tangent by converting the equation of the line into the general form which is $y=mx+c$. We will then differentiate the equation of the ellipse and substitute the value of the slope to get the value of $x$ in terms of $y$and then simplify to get the required points on the ellipse.

Complete step by step solution:
We have the equation of ellipse as $4{{x}^{2}}+9{{y}^{2}}=1$.
The equation of the line is $8x=9y$.
We can see the ellipse and the line on the graph as:

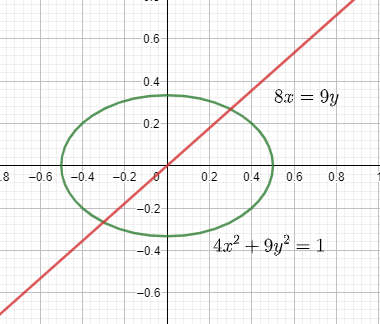
Now on rearranging the equation, we get:
$\Rightarrow 9y=8x$
On transferring the term $9$ from the left-hand side to the right-hand side, we get:
$y=\dfrac{8x}{9}$
The above equation is in the general form of the equation of line which is $y=mx+c$ given that value of $c=0$.
We can conclude that the slope is $\dfrac{8}{9}$.
Now to get the value of $x$ in terms of $y$, we will differentiate the equation of ellipse with respect to $x$.
On differentiating, we get:
$\Rightarrow \dfrac{d}{dx}\left( 4{{x}^{2}}+9{{y}^{2}}=1 \right)$
We know that $\dfrac{d}{dx}\left( {{x}^{2}} \right)=2x$ therefore, on using the formula, we get:
$\Rightarrow 4\left( 2x \right)+9\left( 2y\dfrac{dy}{dx} \right)=1$
On simplifying, we get:
$\Rightarrow 8x+18y\dfrac{dy}{dx}=0$
Now we know that the slope of the line $m=\dfrac{dy}{dx}$ therefore, on substituting, we get:
$\Rightarrow 8x+18y\left( \dfrac{8}{9} \right)=0$
On simplifying, we get:
$\Rightarrow 8x+16y=0$
On dividing both the sides of the expression by $8$, we get:
$\Rightarrow x+2y=0$
On transferring $4y$ from the left-hand side to the right-hand side, we get:
$\Rightarrow x=-2y$
Now we have got the value of $x$ in terms of $y$.
On substituting this value in the equation of ellipse, we get:
$\Rightarrow 4{{\left( -2y \right)}^{2}}+9{{y}^{2}}=1$
On squaring, we get:
$\Rightarrow 4\left( 4{{y}^{2}} \right)+9{{y}^{2}}=1$
On simplifying, we get:
$\Rightarrow 16{{y}^{2}}+9{{y}^{2}}=1$
On adding the terms, we get:
$\Rightarrow 25{{y}^{2}}=1$
On transferring $25$ from the left-hand side to the right-hand side, we get:
$\Rightarrow {{y}^{2}}=\dfrac{1}{25}$
On taking the square root, we get:
$\Rightarrow y=\pm \dfrac{1}{5}$
Now we know that $x=-2y$
Therefore, on substituting, we get:
$\Rightarrow x=-2\left( \pm \dfrac{1}{5} \right)$
On simplifying, we get:
$\Rightarrow x=\mp \dfrac{2}{5}$
Therefore, the points are $\left( \dfrac{-2}{5},\dfrac{1}{5} \right)$ and $\left( \dfrac{2}{5},\dfrac{-1}{5} \right)$.
From the graph below we can see that the points $F=\left( \dfrac{-2}{5},\dfrac{1}{5} \right)$ and $G=\left( \dfrac{2}{5},\dfrac{-1}{5} \right)$ are points on the ellipse $4{{x}^{2}}+9{{y}^{2}}=1$ whose tangents are parallel to the line $8x=9y$.

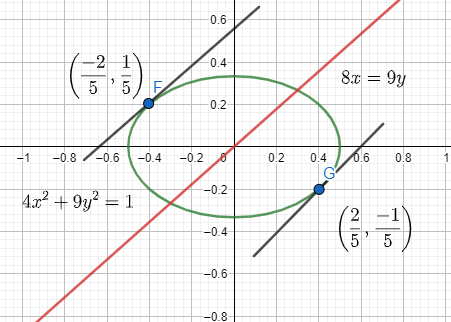
Note: It is to be remembered that the slope of the line refers to the inclination of the line. It tells us the steepness of the line. It is also called the gradient. It is to be remembered that the general equation of an ellipse is $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$, where $a$ represents half the length of the major axis and $b$ represents half the length of the minor axis.