Question

How do you find the period of $y=\cot \left( 2\dfrac{x}{3} \right)$?

Answer 1

Hint: Firstly we need to consider the graph of the function $y=\cot x$ and determine its period. Then by scaling the graph of $y=\cot x$, we will obtain the graph of the given function, that is, $y=\cot \left( 2\dfrac{x}{3} \right)$. From that graph, the required period can be easily determined.

Complete step by step solution:
The function given in the above question is
$\Rightarrow y=\cot \left( 2\dfrac{x}{3} \right)$
We see that the above function is similar to the function $y=\cot x$. The graph of the function $y=\cot x$ is given as

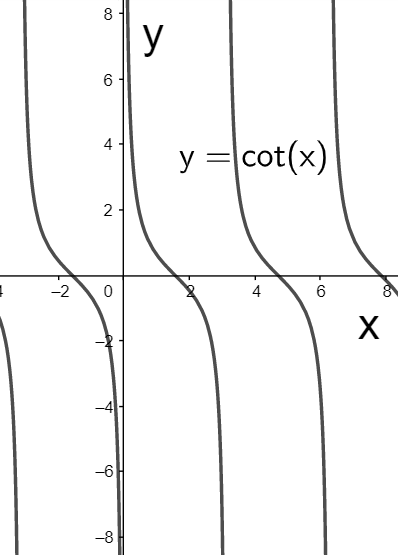
The graph cuts the x-axis at the points $\left( -\dfrac{\pi }{2},0 \right);\left( \dfrac{\pi }{2},0 \right);\left( \dfrac{3\pi }{2},0 \right).......$. Therefore, its period can be given by
$\begin{align}
  & \Rightarrow T=\dfrac{\pi }{2}-\left( -\dfrac{\pi }{2} \right) \\
 & \Rightarrow T=\dfrac{\pi }{2}+\dfrac{\pi }{2} \\
 & \Rightarrow T=\pi .......(i) \\
\end{align}$
So the period of $y=\cot x$ is $\pi $.
Now, the equation $y=\cot \left( 2\dfrac{x}{3} \right)$ can also be written as
$\Rightarrow y=\cot \left( \dfrac{x}{\dfrac{3}{2}} \right)$
Comparing $y=\cot x$, we see that the only change is that the independent variable $x$ is divided by $\dfrac{3}{2}$. So the graph of $y=\cot \left( 2\dfrac{x}{3} \right)$ can be obtained by expanding the graph of $y=\cot x$ in the horizontal direction by $\dfrac{3}{2}$ units as shown below.

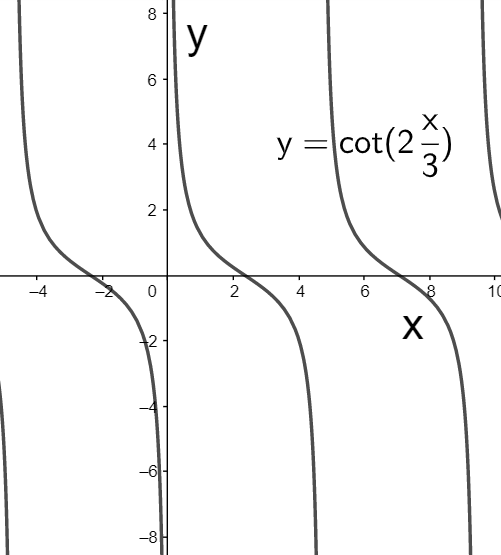
Since the graph of $y=\cot x$ is expanded by $\dfrac{3}{2}$ units, so its period must also be expanded by the same amount, that is, if the period of $y=\cot \left( 2\dfrac{x}{3} \right)$ is $T'$, then it can be given by
$\Rightarrow T'=\dfrac{3}{2}T$
Substituting (i) in the above equation, we get
$\begin{align}
  & \Rightarrow T'=\dfrac{3}{2}\pi \\
 & \Rightarrow T'=\dfrac{3\pi }{2} \\
\end{align}$
Hence, the period of $y=\cot \left( 2\dfrac{x}{3} \right)$ is equal to $\dfrac{3\pi }{2}$.

Note:
For solving these types of questions, we don’t necessarily need the help of the graphs. The graphs only make our work easier. But if we can’t remember them, then we must remember the period of the trigonometric functions. The period of the sine and the cosine functions is equal to $2\pi $, while that of the tangent and the cotangent functions is equal to $\pi $. Then doing the required scaling on the period, we can obtain the period of any trigonometric function.