Question

Find the perimeter of the isosceles right angled triangle shown in the figure if the length of its hypotenuse is given to be equal to \[8\sqrt{2}\].

A. 8
B. \[8+8\sqrt{2}\]
C. \[8+16\sqrt{2}\]
D. 16
E. \[16+8\sqrt{2}\]

Answer 1

Hint: To calculate the perimeter, we need to know the length of its all three sides. Two sides of an isosceles triangle are equal, so assume the length of the two equal sides to be $x$. Using $'x'$ calculate the length of the hypotenuse and equate that to the given value to form an equation in $x$ and then solve for $x$. After finding all the three sides, calculate their sum to get the perimeter.

Complete step-by-step answer:
Given triangle is a right isosceles triangle,

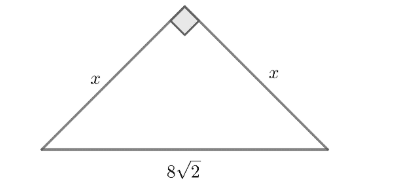
We need to find the perimeter of the given triangle.
Perimeter of a triangle is defined as the sum of the lengths of all the sides of a triangle.
So, for finding the perimeter, we need to find the length of all the sides of the triangle.
Length of its hypotenuse is given, so we need to find the length of the other two sides.
We know that the length of two sides are equal in an isosceles triangle.
Let the length of the equal sides be $x$.
We know in a right triangle:
${{\left( Hypotenuse \right)}^{2}}={{\left( Perpendicular \right)}^{2}}+{{\left( Base \right)}^{2}}$
Putting the values, we will get,
$\begin{align}
  & \Rightarrow {{\left( 8\sqrt{2} \right)}^{2}}={{\left( x \right)}^{2}}+{{\left( x \right)}^{2}} \\
 & \Rightarrow 128={{x}^{2}}+{{x}^{2}} \\
 & \Rightarrow 128=2{{x}^{2}} \\
\end{align}$
Dividing both sides of equation by ‘2’, we will get,
$\Rightarrow 64={{x}^{2}}$
Taking positive square root both sides of the equation, we will get,
$\Rightarrow 8=x$
We have taken positive square roots because the length of a side can’t be negative.
Now, perimeter = sum of all the three sides
$\begin{align}
  & =8\sqrt{2}+x+x \\
 & =8\sqrt{2}+8+8 \\
 & =8\sqrt{2}+16 \\
\end{align}$
Hence, the required perimeter is \[16+8\sqrt{2}\] and option (E) will be our answer.

Note:

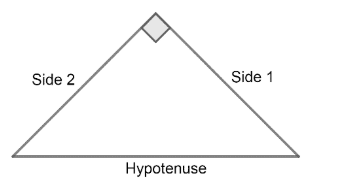
We know that two sides of an isosceles triangle are the same and this length is different from the length of the third side. In our solution we have assumed the length of side 1 and side 2 be equal. Why haven’t we assumed length of hypotenuse and any of side 1 or side 2 be equal?
Because we know that,
${{\left( Hypotenuse \right)}^{2}}={{\left( Perpendicular \right)}^{2}}+{{\left( Base \right)}^{2}}$
So, the length of the hypotenuse will always be greater than the other two sides. It can’t be equal to the length of any of the sides.