Question

Find the perimeter of a sector whose radius and central angle are 18 cm and $210^{\circ}$ respectively.

Answer 1

Hint: First draw the diagram of the sector with given values and conditions. Use the arc length formula and the two radii to find the perimeter. Arc length $s=r \theta $. Before solving, convert the angle of degrees in radians. The addition of arc length and the two radii will give us to find the perimeter.

Complete step-by-step answer:
Let us draw the sector with radius of 18 cm and angle $210{}^\circ $

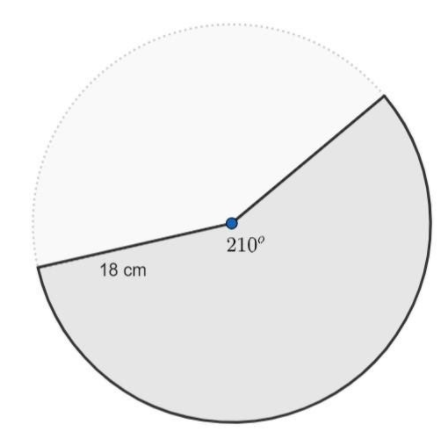
Here, in this diagram you can see, that we have an angle of 210 degree and a radius of 21 cm.
Now, in order to find the perimeter of the sector we must know the formula for arc length and the radius. As we already have the radius, we need to know the arc length.
We know, the arc length $s=r\theta $.......... (i)
Where, $s$ is the arc length, $r$ is the radius and $\theta $ is the angle in degrees
We need the angle in radians, so in order to change the angle from degree to radians, divide the angle by 180 and multiply it with $\pi $.
Let us consider the angle in degree as ${{\theta }_{d}}$ and angle in
$\begin{align}
  & {{\theta }_{r}}=\dfrac{\pi }{180}\times {{\theta }_{d}} \\
 & =\dfrac{{{\theta }_{d}}}{180\times 2}\times 2\pi \\
 & =\dfrac{{{\theta }_{d}}}{360}\times 2\pi
\end{align}$
Now, if we substitute the above equation in equation (i), we get
$\begin{align}
  & s=r\cdot \left( \dfrac{{{\theta }_{d}}}{360}\times 2\pi \right) \\
 & =\dfrac{{{\theta }_{d}}}{360}\times 2\pi r
\end{align}$
Here, let us find the perimeter of the sector,
Perimeter of the sector = arc length + 2 radii
$\begin{align}
& =\dfrac{{{\theta }_{d}}}{360}\times 2\pi r+2r \\
\end{align}$
Now, let us take 2r common,
Perimeter of the sector = $2r\left( \dfrac{{{\theta }_{d}}}{360}\times \pi +1 \right)$
Substitute the given values of the angle and the radius and find the perimeter
Perimeter of the sector $=2\left( 18 \right)\left( \dfrac{210\pi }{360}+1 \right)$
$\begin{align}
& =2\left( 18 \right)\left( \dfrac{7\pi }{12}+1 \right) \\
& =2\left( 18 \right)\left( 0.5833\pi +1 \right) \\
 & =2\left( 18 \right)\left( 2.8325 \right) \\
 & =101.97 \\
 & \approx 102 \\
\end{align}$
Hence, the perimeter for the sector with radius 21 cm and $210^{\circ}$ angle is approximately equal to 102 cm.

Note: Here, in this question, the perimeter should be in cm because all the other values are in cm and the angle is changed to radians. Also, remember to put the units after different values. Here we add 2r as the sector is to be a close shape and perimeter is the sum of all sides together.