Question

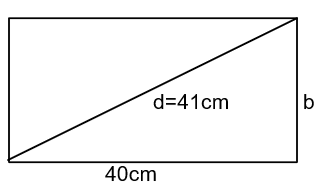
Find the perimeter of a rectangle whose length is $40cm$ and diagonal is $41cm$.

Answer 1

Hint: The area can be defined as the space occupied by a flat surface of an object. The area is the number of unit squares closed by figure. Perimeter is the total length of the sides of the two dimensional shape. Perimeter is always less than the area of the given figure. Because the perimeter is outer and the area is inner property.

Complete step-by-step solution:

Given,
Length of the rectangle, $l=40cm$
Diagonal of the rectangle, $d=41cm$
Breadth of the plot, $b=?$
As we know that.
Diagonal of rectangle is given by,
$\therefore d=\sqrt{l^2+b^2}$
So,
$\therefore b=\sqrt{d^2-l^2}$
Put the values
$\Rightarrow b=\sqrt{{41}^2-{40}^2}$
Simplify
$\Rightarrow b=\sqrt{81}$
$\Rightarrow b=9cm$
Now
Parameter of rectangle
As we know that
$\therefore P=2(l+b)$
Put the values
$$\Rightarrow P=2(40+9)$$
Simplify
$$\Rightarrow P=2\times 49$$
$$\Rightarrow P=98c{m}^2$$
The parameter of the rectangle is $98c{m}^2$

Note: Perimeter is the sum of all sides. Where the area is space occupied by the closed figure. Volume is how much an object will hold. There is not any direct relation between area and perimeter. But both of them totally depend on dimensions of the figure.