Question

Find the perimeter of a rectangle in which length is 2 m 25 cm and breadth is 1 m 50 cm.

Answer 1

Hint: The perimeter of a rectangle is the total length of its boundaries. So first convert both length and breadth in either meter or centimeter using $1{\text{ m}} = 100{\text{ cm}}$. Then apply the formula of perimeter of rectangle i.e. $2\left( {l + b} \right)$, where $l$ and $b$ are length and breadth respectively, to get the final answer.

Complete step-by-step answer:
According to the question, the length of the rectangle is 2 m 25 cm and the breadth of the rectangle is 1 m 50 cm. Let they be denoted as $l$ and $b$ respectively.
We know that meter and centimetre are related by the formula:
$ \Rightarrow 1{\text{ m}} = 100{\text{ cm}}$
Using this formula for both $l$ and $b$, we’ll get:
$
   \Rightarrow l = 2 \times 100 + 25{\text{ cm}} = 225{\text{ cm }}.....{\text{(1)}} \\
   \Rightarrow b = 1 \times 100 + 50{\text{ cm}} = 150{\text{ cm }}.....{\text{(2)}}
 $
This is shown in the below diagram:

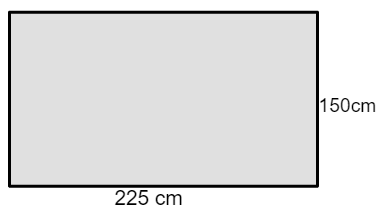
Further, we know that the formula for perimeter of a rectangle is given as:
$ \Rightarrow P = 2\left( {l + b} \right)$
Applying this formula and putting the values of $l$ and $b$ from equation (1) and (2) respectively, we’ll get:
\[
   \Rightarrow P = 2 \times \left( {225 + 150} \right){\text{ cm}} \\
   \Rightarrow P = 2 \times 375{\text{ cm}} \\
   \Rightarrow P = 750{\text{ cm}}
 \]
We can also convert it into meters. This will be:
\[
   \Rightarrow P = \dfrac{{750}}{{100}}{\text{ m}} \\
   \Rightarrow P = 7.5{\text{ m}}
 \]

Thus the perimeter of the rectangle is 750 cm or 7.5 meter.

Additional Information: If the two dimensions of a rectangle are given, its area can also be easily calculated. The area of a rectangle is given by the formula:
$ \Rightarrow A = l \times b$, where $l$ and $b$ are length and breadth respectively.

Note: When both the dimensions of a rectangle are the same then it is no longer a rectangle. Instead it becomes a square. In square, length and breadth are the same. Its area is calculated by the formula $A = {\left( {{\text{Side}}} \right)^2}$ and perimeter is calculated by the formula $P = 4 \times {\text{Side}}$.