Question

Find the number of zero polynomials from the graph?

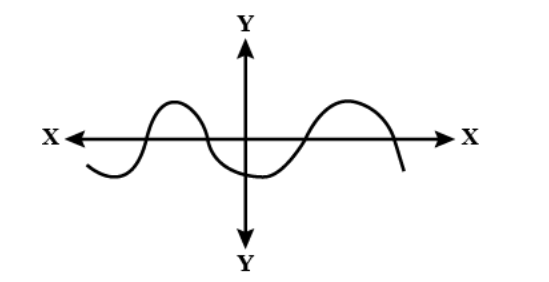
Answer 1

Hint: The zeros of the polynomial are the points where the graph intersects the x-axis.The zeros of a polynomial are the solutions to the equation \[p(x)=0\], where \[p(x)\]represents the polynomial. If we graph this polynomial as \[y=p(x)\], then you can see that these are the values of x where \[y=0\]. In other words, they are the x-intercepts of the graph.

Complete step-by-step answer:
A root or a zero of a polynomial are the value(s) of X that cause the polynomial to = 0 (or make Y=0). It is an X-intercept. The root is the X-value, and zero is the Y-value. It is not saying that imaginary roots = 0.
Consider a polynomial \[p(x)\], which is graphed below.

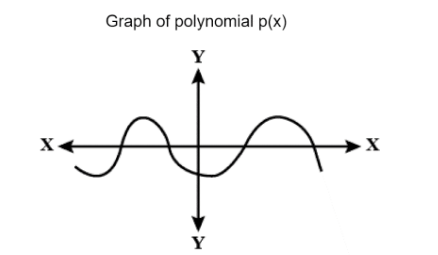
To answer this question, you want to find the \[x-\]intercepts. To find these, look for where the graph passes through the \[x-\]axis (the horizontal axis).

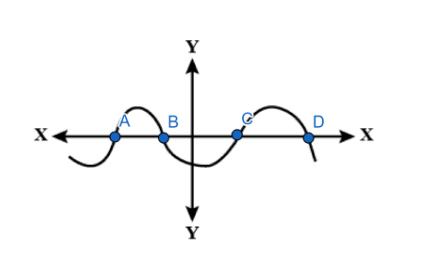
In the given graph, the curve intersects the x-axis at four points, therefore, the number of zeros of the polynomial are 4.
The steps to find zeros of polynomial are:
1.Arrange the polynomial in descending order.
2.Write down all the factors of the constant term. These are all the possible values of p.
3.Write down all the factors of the leading coefficient. ...
4.Write down all the possible values of . ...
5.Use synthetic division to determine the values of for which P( ) = 0

Note: While here, all the zeros were represented by the graph actually crossing through the \[x-\]axis, this will not always be the case. Like any constant value, the value 0 can be considered as a (constant) polynomial, called the zero polynomial. It has no nonzero terms, and so, strictly speaking, it has no degree either. As such, its degree is usually undefined.