Question

Find the number of ways in which 8 people numbered from 1 to 8 can be seated in a circular table so that 1 always sits between 2 and 3.

Answer 1

Hint: We can calculate the total number of ways all the persons can be seated on a circular table and then find the ways that 1 always sits between 2 and 3, by grouping them together.
For n number of people, the seating arrangements are given by (n-1)!

Complete step-by-step answer:

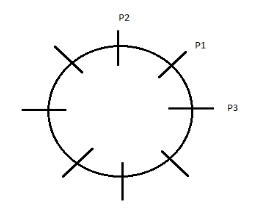
As there are 8 persons, the total number of ways in which they can be seated is given as:
(8 – 1) ! = 7!
If we group together P1, P2, and P3 with P1 between the other two, it can be done in 2 different ways i.e.
P2 P1 P3 and P3 P1 P2,
Thus the number of ways of arrangement of these three is 2! ___________ (1)
Now, as these 3 persons are grouped together, they will be counted as a single person, thus rest of the person's needs be arranged are:
P1 (P1+ P2 + P3) + P4 + P5 + P6 + P7+ P8 = 6 persons
The number of ways in which 6 people can be arranged is given as:
(6 – 1)! = 5! _________________ (2)
From (1) and (2) the total number of ways in which 8 people numbered from 1 to 8 can be seated in a circular table so that 1 always sits between 2 and 3 is 5! X 2 or 240!.
[As on calculation, it 5! X 2! can also be written as 240]

Note: When asked about the number of arrangements, we generally answer in terms of factorial only.
When we group together a number of people we need to remember that there will be varied arrangements inside the group as well for which we have to find factorial as well and when counting the number of people the group will be counted as a single person.
Different kinds of seating arrangements include circular, linear, rectangular, etc.