Question

Find the number of images formed according to given case

A. 8,9
B. 9,8
C. 9,9
D. 8,8

Answer 1

Hint: Define image formation in a mirror. Obtain the mathematical expression for the number of images formed in two plane mirrors if the mirrors are inclined to each other. The number of images will depend on the angle between the mirror and the position of the object between the mirror. Use this concept to find the number of images formed in the given two cases.

Complete step by step answer:
When two plane mirrors are inclined to each other at an angle, more than one image is formed. The number of images formed depends on the angle between the two mirrors and the position of the object between two mirrors.
Now, if the angle between the mirrors is A, then the number of image formed is $n=\left( \dfrac{{{360}^{0}}}{A} \right)-1$ , when $\left( \dfrac{{{360}^{0}}}{A} \right)$ is an even integer.
If $\left( \dfrac{{{360}^{0}}}{A} \right)$ is an odd integer, the number of images formed depends on the position of the object between the mirrors. If the object is symmetrically placed between the mirrors, the number of images formed will be $n=\left( \dfrac{{{360}^{0}}}{A} \right)-1$. When the object is asymmetrically placed between the mirrors, the number of images formed will be, $n=\left( \dfrac{{{360}^{0}}}{A} \right)$.
Again, if $\left( \dfrac{{{360}^{0}}}{A} \right)$ is a fraction, then the number of images formed will be equal to its integral part.
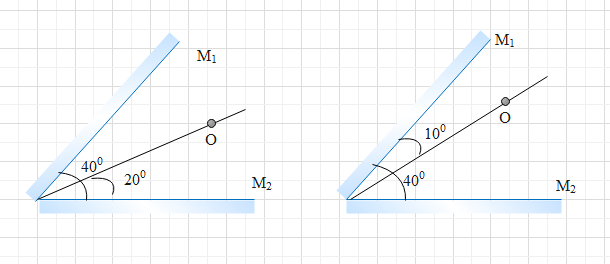
Now, in the question, the angle between the image is ${{40}^{0}}$ .
So,
$\left( \dfrac{{{360}^{0}}}{{{40}^{0}}} \right)=9$ , which is an odd number.
So, in the first case, the object is symmetrically placed between the mirrors. So, the number of images formed will be,
$n=\left( \dfrac{{{360}^{0}}}{{{40}^{0}}} \right)-1=9-1=8$
In the second case, the object is asymmetrically placed between the mirrors. So, the number of images formed will be,
$n=\left( \dfrac{{{360}^{0}}}{{{40}^{0}}} \right)=9$
So, the number of image forms will be 8 in the first case and 9 in the second case.
The correct option is (A)

Note: The two given cases look similar to each other, because the angle between the mirrors are the same. But the value of $\left( \dfrac{{{360}^{0}}}{A} \right)$is odd and because of this the number of images formed will also depend on the position of the object. Remember the condition with which the expression changes.