Question

Find the number of geometrical isomers in $\left[\text{M}{\text{A}}_3{\text{B}}_3\right]$ .

Answer 1

Hint: The geometrical isomers of $\text{M}{\text{A}}_3{\text{B}}_3$ will be known if we somehow get to know the coordination number of the compound. After knowing the coordination number of the compound, we can draw its geometrical isomers. The compound given is octahedral.

Complete Step-by-Step solution :
By looking at the chemical compound provided to us in the question, we can observe that $M$ is forming six bonds in total. $M$ is forming three bonds with $A$ and three bonds with $B$ .
Also, the coordination number will be $6$ .
Since, the coordination number is $6$ , the isomers of the above stated chemical compound will be octahedral in shape.
So, now let us draw the two octahedral geometric isomers of $\text{M}{\text{A}}_3{\text{B}}_3$

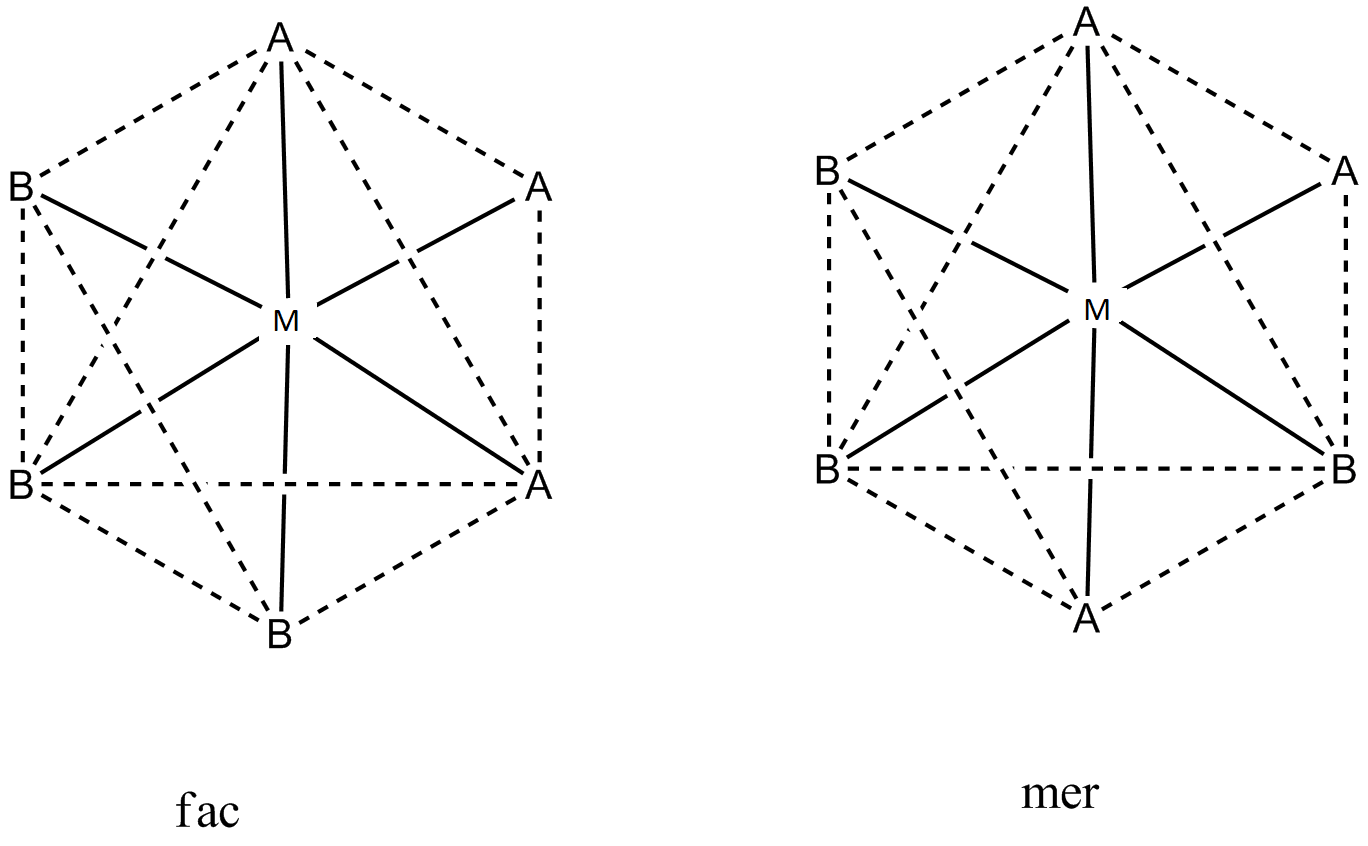
These are the two possible geometrical isomers of $\text{M}{\text{A}}_3{\text{B}}_3$ in an octahedral shape.
The fac molecule is also called as cis molecule. The full abbreviated form of fac is facial and that of mer is meridional.
The two ligands in cis molecules are on the same side of the complex. The comparable ligands in trans molecules are on the opposite sides of the molecules as shown in the figure.
The geometric isomer is also known as cis-trans isomer.

Note:
Isomerism is a phenomenon in which more than one compound has different chemical structures, but the same chemical formula. Chemical compounds that have identical chemical formulas but vary in properties are called isomers and the arrangement of atoms in the molecule. Geometric isomerism is a form of stereoisomerism with the same molecular formula and structure, but the relative arrangement of atoms differs. Due to the various possible geometric arrangements for the ligand, this form of isomerism occurs.