
Find the number of diagonals in the polygon of n sides.
Answer
604.5k+ views
Hint: First write definitions of polygon and look at the possible sides and vertices. Now look at the definition of the diagonal of a polygon. Now list the possible vertices for which we can get a diagonal. Now add all the possibilities in an intelligent way to find the total number of diagonals. After getting a number of diagonals, check the values for any known polygon for verification.
Complete step-by-step answer:
Polygon: - In general geometry polygon is defined as a plane figure that is described by a finite number of straight line segments connected to form a closed polygon chain. It is also defined as the solid region of a plane bounded by a bunch of line segments. Also called bounded circuit.
Diagonal of polygon: - Diagonal is a line segment which joins any two non – consecutive vertices. Consecutive vertices from edges so only 2 diagonals possible. For any convex polygon diagonals lie inside the polygon. Example: - square.
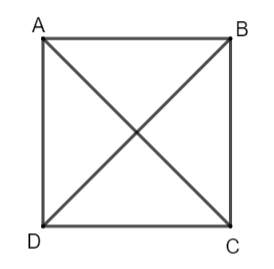
Take n – sided polygon ABCDE.
Pick any vertex of the polygon. Now we have (n - 1) other vertices to form a line segment. We know adjacent vertices from edges not diagonal. Any vertex has 2 adjacent vertices one after, one before. By subtracting these 2 vertices, the possibilities become:
(n - 3) possibilities
As there are n vertices for n sided polygon.
By multiplying with n for possibilities, we get:
n (n - 3)
We are counting each diagonal twice because AC is connected at A and CA is counted as C but both are the same.
This is done with every diagonal.
So, by dividing 2 for the possibilities, we get:
Number of diagonals = \[\dfrac{n\left( n-3 \right)}{2}\] - (1)
Verification for square: n = 4
By substituting n = 4 in equation (1), we get,
Number of diagonals = \[\dfrac{4\left( 4-3 \right)}{2}=\dfrac{4\times 1}{2}=2\].
So, the number of diagonals for squares is 2 which is true. So, the formula (1) is correct.
Therefore, the number of diagonals for n sided polygon are given by \[\dfrac{n\left( n-3 \right)}{2}\].
Note: Be careful don’t forget to divide by 2 because of repeated counting of each diagonal. Alternate method is to use minor tricks. It is described as follows: Every two vertices form an edge or diagonal. Thus these are \[{}^{n}{{C}_{2}}\] number of pairs which is equal to sum of number of edges and diagonal. So, \[{}^{n}{{C}_{2}}\] - number of edges is number of diagonals where n is number of edges. So, number of diagonals are \[{}^{n}{{C}_{2}}\] - n, which is simplified as \[\dfrac{n\left( n-1 \right)}{2}\] - n which can be written as \[\dfrac{n\left( n-3 \right)}{2}\], which is same result as above.
Complete step-by-step answer:
Polygon: - In general geometry polygon is defined as a plane figure that is described by a finite number of straight line segments connected to form a closed polygon chain. It is also defined as the solid region of a plane bounded by a bunch of line segments. Also called bounded circuit.
Diagonal of polygon: - Diagonal is a line segment which joins any two non – consecutive vertices. Consecutive vertices from edges so only 2 diagonals possible. For any convex polygon diagonals lie inside the polygon. Example: - square.

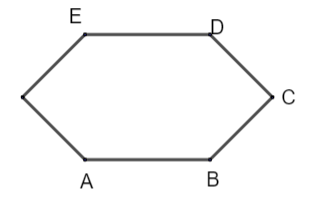
Take n – sided polygon ABCDE.

Pick any vertex of the polygon. Now we have (n - 1) other vertices to form a line segment. We know adjacent vertices from edges not diagonal. Any vertex has 2 adjacent vertices one after, one before. By subtracting these 2 vertices, the possibilities become:
(n - 3) possibilities
As there are n vertices for n sided polygon.
By multiplying with n for possibilities, we get:
n (n - 3)
We are counting each diagonal twice because AC is connected at A and CA is counted as C but both are the same.
This is done with every diagonal.
So, by dividing 2 for the possibilities, we get:
Number of diagonals = \[\dfrac{n\left( n-3 \right)}{2}\] - (1)
Verification for square: n = 4
By substituting n = 4 in equation (1), we get,
Number of diagonals = \[\dfrac{4\left( 4-3 \right)}{2}=\dfrac{4\times 1}{2}=2\].
So, the number of diagonals for squares is 2 which is true. So, the formula (1) is correct.
Therefore, the number of diagonals for n sided polygon are given by \[\dfrac{n\left( n-3 \right)}{2}\].
Note: Be careful don’t forget to divide by 2 because of repeated counting of each diagonal. Alternate method is to use minor tricks. It is described as follows: Every two vertices form an edge or diagonal. Thus these are \[{}^{n}{{C}_{2}}\] number of pairs which is equal to sum of number of edges and diagonal. So, \[{}^{n}{{C}_{2}}\] - number of edges is number of diagonals where n is number of edges. So, number of diagonals are \[{}^{n}{{C}_{2}}\] - n, which is simplified as \[\dfrac{n\left( n-1 \right)}{2}\] - n which can be written as \[\dfrac{n\left( n-3 \right)}{2}\], which is same result as above.
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
What is the median of the first 10 natural numbers class 10 maths CBSE

Which women's tennis player has 24 Grand Slam singles titles?

Who is the Brand Ambassador of Incredible India?

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

A moving boat is observed from the top of a 150 m high class 10 maths CBSE




