Question

How do you find the number of complex, real and rational roots of \[4{{x}^{5}}-5{{x}^{4}}+{{x}^{3}}-2{{x}^{2}}+2x-6=0\]?

Answer 1

Hint: The degree of a polynomial is the highest power of the variable of the equation. The degree is always a positive integer. The roots of a function are the values of the variable at which the functional value is equal to zero. For a polynomial expression, the maximum number of roots including both real and complex roots is equal to the degree of the polynomial.

Complete step-by-step solution:
The given equation is \[4{{x}^{5}}-5{{x}^{4}}+{{x}^{3}}-2{{x}^{2}}+2x-6=0\]. we can see that the degree of the given polynomial function is 5, so the maximum number of roots the polynomial has is 5. This included all imaginary and real roots it has.
As this is a polynomial function, this is always continuous and differentiable. We find the number of real roots by plotting the graph of the polynomial. The number of times the graph crosses or touches X-axis is the number of real roots it has.
The graph of the function is as follows

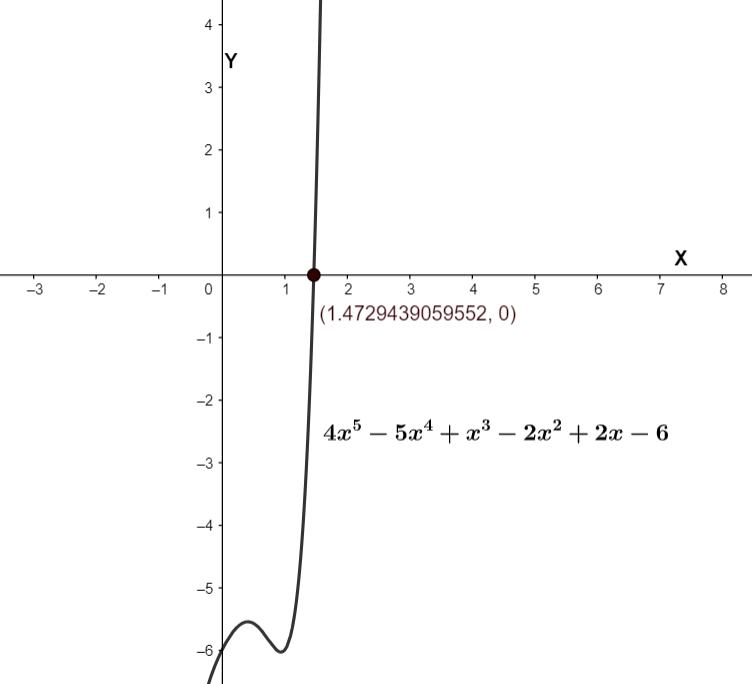
We can see that the graph of the polynomial crosses the X-axis only once, hence the number of real roots it has is one. So, the number of imaginary or complex roots it has is \[5-1=4\].

Note: Generally finding the complex roots of a polynomial equation is very difficult. So, a question to find the value of the imaginary root will not be asked. But the number of roots is very common. Here, we are also asked the number of rational roots, but as there are not any. It is zero.