Question

Find the net elongation of the composite rod (Assume A = cross section of each rod).

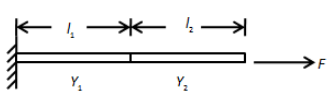
A. \[FA\left( {\dfrac{{{l_1}}}{{{Y_1}}} + \dfrac{{{l_2}}}{{{Y_2}}}} \right)\]
B. \[\dfrac{F}{A}\left( {\dfrac{{{l_1}}}{{{Y_1}}} + \dfrac{{{l_2}}}{{{Y_2}}}} \right)\]
C. \[\dfrac{F}{A}\dfrac{{{l_1}{l_2}}}{{{Y_1} + {Y_2}}}\]
D. \[\dfrac{{{Y_1}{Y_2}\left( {{l_1} + {l_2}} \right)}}{{{l_1}{Y_1} + {l_2}{Y_2}}}\]

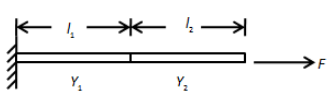
Answer 1

Hint:Recall the expression for the Young’s modulus and express the elongation produced in the both rods separately. The change in the length of the composite rod is equal to the sum of elongation of the respective lengths of the rod. Substitute the elongations of the both lengths and determine the net elongation of the composite rod.

Formula used:
\[Y = \dfrac{{F\,l}}{{A\,\Delta l}}\]
Here, F is the applied force, l is the original length of the rod, A is the cross-sectional area of the rod and \[\Delta l\] is the change in the length of the rod.

Complete step by step answer:
We assume there is a small elongation \[\delta {l_1}\] in the rod of length \[{l_1}\] and \[\delta {l_2}\] is the small elongation in the rod of length \[{l_2}\] by the application of applied force F.
We have the expression for the Young’s modulus is,
\[Y = \dfrac{{F\,l}}{{A\,\Delta l}}\]
Here, F is the applied force, l is the original length of the rod, A is the cross-sectional area of the rod and \[\Delta l\] is the change in the length of the rod.

We can express the small elongation produced in the rod of length \[{l_1}\]using the above equation as,
\[\delta {l_1} = \dfrac{{F\,{l_1}}}{{A\,{Y_1}}}\] …… (1)
We can also express the small elongation produced in the rod of length \[{l_2}\]using the above equation as,
\[\delta {l_2} = \dfrac{{F\,{l_2}}}{{A\,{Y_2}}}\] …… (2)
These small elongations in the lengths \[{l_1}\] and \[{l_2}\] will entirely contribute to change in the length of the composite rod. The change in the length of the composite rod is,
\[\Delta l = \delta {l_1} + \delta {l_2}\]
Using equation (1) and (2) in the above equation, we get,
\[\Delta l = \dfrac{{F\,{l_1}}}{{A\,{Y_1}}} + \dfrac{{F\,{l_2}}}{{A\,{Y_2}}}\]
\[ \therefore \Delta l = \dfrac{F}{A}\left( {\dfrac{{{l_1}}}{{\,{Y_1}}} + \dfrac{{{l_2}}}{{{Y_2}}}} \right)\]

So, the correct answer is option B.

Note:The composite rod is formed by joining the two metal rods of different materials. The Young’s modulus depends on the property of the material and therefore, the Young’s modulus is different for the two rods. The elongation produced in the rod depends on the Young’s modulus of the rod and therefore, the elongation is different for the two rods.