Question

Find the net displacement of a particle from its starting Point it undergoes three successive displacements given \[\overrightarrow {{S_1}} = 20m\] , ${45^ \circ }$ west of north, $\overrightarrow {{S_2}} = 15m$ , ${30^ \circ }$ north of east $\overrightarrow {{S_3}} = 20m$ due south.

Answer 1

Hint: This is the problem from the topic of kinematics. For finding the net displacement find the individual value of the given vectors keeping in mind their angles and positions. Finally according to vector addition law the sum of all the given vectors we will give our required net displacement.

Complete answer:
The position vector is used to describe the location of a body. When it comes to characterising a body's motion, knowing its position is essential. In general, an object's position vector is measured from the origin.

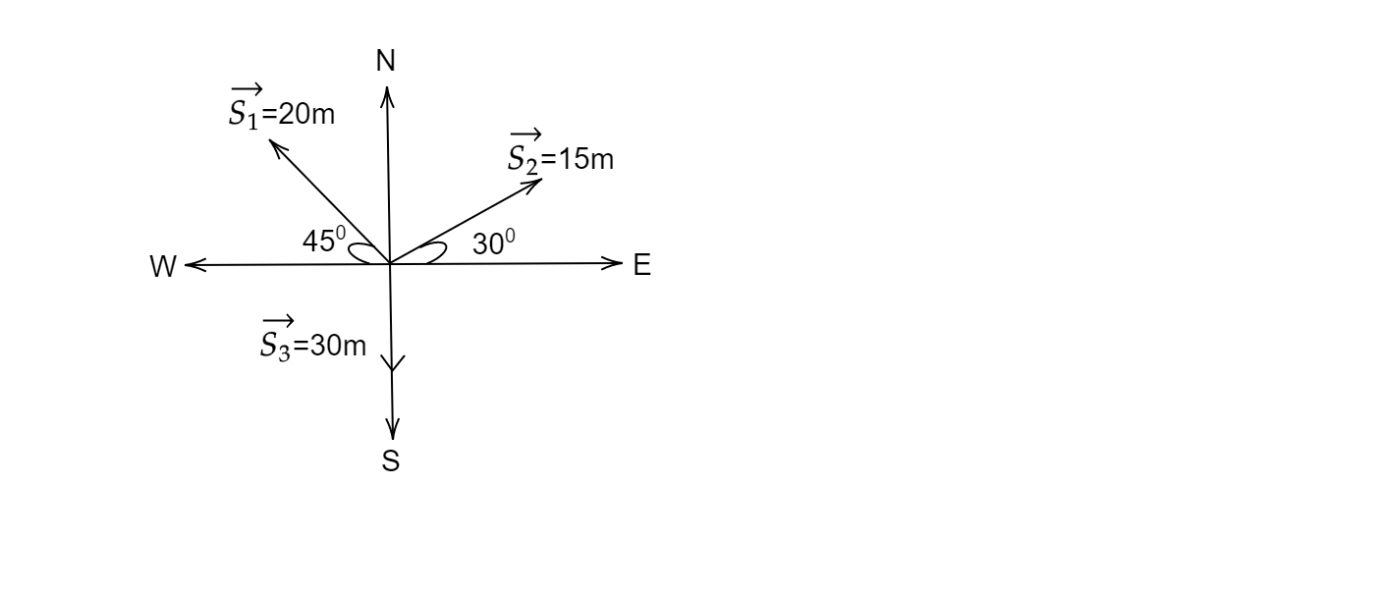
The displacement vector is defined as the change in an object's position vector. Here we have been given three displacements in vector form which are in different direction and are making different angle. All of them are starting from the origin.

From the diagram taking components of \[\overrightarrow {{S_1}} \] and $\overrightarrow {{S_2}} $, and putting value of their angle and the sign according to their position.

Components of \[\overrightarrow {{S_1}} \] will be,
\[\overrightarrow {{S_1}} = - 20\cos {45^ \circ } + 20\sin {45^ \circ }\]
\[ \Rightarrow \overrightarrow {{S_1}} = \dfrac{{ - 20}}{{\sqrt 2 }}\widehat i + \dfrac{{20}}{{\sqrt 2 }}\widehat j\]
Components of $\overrightarrow {{S_2}} $ will be,
$\overrightarrow {{S_2}} = 15\cos {30^ \circ } + 15\sin {30^ \circ }$
$ \Rightarrow \overrightarrow {{S_2}} = 15 \times \dfrac{{\sqrt 3 }}{2}\widehat i + 15 \times \dfrac{1}{2}\widehat j$
For $\overrightarrow {{S_3}} $ we get,
$ \Rightarrow \overrightarrow {{S_3}} = - 30\widehat j$
Therefore the net displacement will be equal to the sum of all three displacement.
$\overrightarrow S = \overrightarrow {{S_1}} + \overrightarrow {{S_2}} + \overrightarrow {{S_3}} $
$\overrightarrow S = \left( {\dfrac{{15\sqrt 3 }}{2} - 10\sqrt 2 } \right)\widehat i + \left( {10\sqrt 2 + 7.5 - 30} \right)\widehat j$
$ \Rightarrow \left| S \right| = \sqrt {{{\left( {\dfrac{{15\sqrt 3 }}{2} - 10\sqrt 2 } \right)}^2} + {{\left( {10\sqrt 2 + 7.5 - 30} \right)}^2}} $
$ \Rightarrow \left| S \right| = 8.44m$
Hence the net displacement of a particle is $S = 8.44m$

Note:
The most important requirement for adding two vectors is that they should be like vectors, that is, they should have the same dimensions and units. The shortest distance between two sites is also known as displacement.