Question

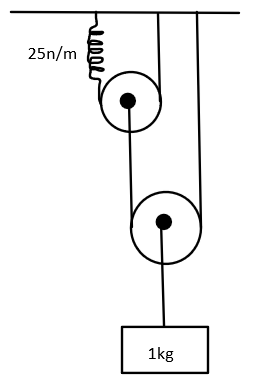
Find the natural frequency of oscillation of the system as shown in the figure. Pulleys are massless and frictionless. Spring and string are also massless. (Take ${\pi ^2} = 10$)

A) $\dfrac{\pi }{2}\,Hz$
B) $\sqrt \pi \,Hz$
C) $\dfrac{{10}}{{\sqrt \pi }}\,Hz$
D) $\pi \,Hz$

Answer 1

Hint: You can easily solve this question by considering how much each pulley, thus each string and thus the spring will move when the mass goes down by a length of $x$. Using this, you can write the force on the string as ${F_{spring}}\, = \, - k{x_{acting}}$ and use the same to find the frequency of oscillation.

Complete step by step answer:
We will approach the solution exactly as told in the hint section of the solution to the question.
Let’s first see how the force applied due to the mass of $1\, kg$ is being divided between the pulleys and among the strings and spring.
Let us assume that the force is $F$.
We can see that the lower pulley has two strings to support the weight. Hence, the force gets equally distributed between them. Thus, we can say that both sides now experience a force of magnitude of $\dfrac{F}{2}$.
Now, the upper pulley experiences a total force of $\dfrac{F}{2}$ magnitude, which further gets equally distributed on both sides, thus, we can say that the spring and the string experience an equal force of magnitude $\dfrac{F}{4}$.
Now, we will check what happens when the body moves down by a distance $x$,
When the mass of $1\, kg$ goes down by a distance of $x$, the lower pulley also goes down by the same distance of $x$. Since one side of the string is fixed, it can not move down by the distance $x$, hence, the string attached to the upper pulley goes down by a distance of $2x$. If it happens, the upper pulley would move down by a distance of $2x$. Again, one side of the string is fixed, hence, spring will have to compensate for it by moving a distance of $4x$.
Now, we have found out the force acting on the spring as well as the actual displacement of the spring when the mass goes down by a distance of $x$.
We can write it mathematically as
$\dfrac{F}{4} = - k\left( {4x} \right)$
Further simplifying, we can write it as:
$\Rightarrow F = - 16kx$
The value of spring constant $\left( k \right)$ as given in the question is $25\,n/m$
Substituting the value of spring constant here, we get:
$\Rightarrow F = - \left( {16 \times 25} \right)x$
$\Rightarrow F = - 400x $
Now, we can confidently say that the object performs SHM with $\omega = \sqrt {400} = 20\,rad/s$
We already know that frequency can be given as
$f = \dfrac{\omega }{{2\pi }}$
Substituting in the value of $\omega $ , we get
$\Rightarrow f = \dfrac{{20}}{{2\pi }}$
Simplifying and then putting $10 = {\pi ^2}$(approximation) as told in the question, we get:
$\Rightarrow f = \pi \,Hz$

Hence, the correct option is option (D).

Note:
Many students believe that if the object is moving down by a distance of $x$ each string and spring will do the same, which is a completely wrong assumption and causes them to lose marks. Also, always remember that this is the best approach to solve such questions.