Question

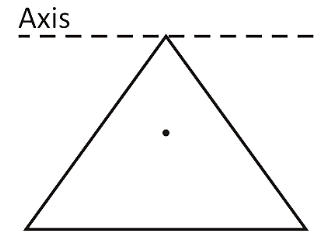
Find the moment of inertia of a thin sheet of mass \[M\] in the shape of an equilateral triangle about an axis as shown in the figure. The length of each side is \[L\].

Answer 1

Hint:First of all, we will use the area of the inertial moment of a triangle around an axis. After that we will find the mass moment of inertia. After that we will find a moment of inertia of the triangle about an axis which passes through the centroid but parallel to one of the sides. Lastly, we will apply parallel axis theorem and manipulate accordingly and make correct substitutions.

Formula used:
The area of the triangle is:
\[\dfrac{1}{2} \times b \times h\]
Where,
\[b\] indicates the base.
\[h\] indicates the altitude.

Complete step by step answer:
In the given question, we are supplied with the following data:
There is a mass \[M\] whose shape is in the form of an equilateral triangle. The length of each side of the triangle is \[L\].The axis is located at the upper vertex in the form of a horizontal line just touching the upper vertex. We are asked to find the moment of inertia about the vertex which is parallel to the base.

Let us proceed to solve the problem.
We know, the inertial moment of a triangle around an axis going around its centroid and parallel to one side is \[\dfrac{{b{h^3}}}{{36}}\].So, the mass moment of inertia of the triangle can be written as \[\dfrac{{b{h^3}}}{{36}} \times \dfrac{M}{A}\].
Where, \[M\] indicates the mass of the shape. \[A\] indicates the area of the triangle.

Moment of inertia of the triangle about an axis which passes through the centroid but parallel to one of the sides, can be written as:
\[\dfrac{{M{h^2}}}{{18}}\]
Now, the axis is shifted to one vertex here, i.e., pushed to a distance \[\dfrac{2}{3}h\].
By the theorem of the parallel axis, the moment of inertia of an object around the centroid along a parallel axis to the axis can be written as:
The sum of the moment of inertia about the centroid and \[M{d^2}\].
Where, \[d\] indicates the distance between the axis and the centroid.
So, we can mathematically write:
$I = \dfrac{{M{h^2}}}{{18}} + M{d^2} \\
\Rightarrow I = \dfrac{{M{h^2}}}{{18}} + M \times {\left( {\dfrac{{2h}}{3}} \right)^2} \\
\Rightarrow I = M{h^2} \times \left( {\dfrac{1}{{18}} + \dfrac{4}{9}} \right) \\
\Rightarrow I = \dfrac{1}{2}M{h^2} \\$
In an equilateral triangle, if we apply the Pythagoras’ theorem, we can easily find the relation of the altitude in terms of the length of the triangle.
${L^2} = {h^2} + {\left( {\dfrac{L}{2}} \right)^2} \\
\Rightarrow {h^2} = {L^2} - \dfrac{{{L^2}}}{4} \\
\Rightarrow {h^2} = \dfrac{{3{L^2}}}{4} \\
\Rightarrow h = \dfrac{{\sqrt 3 }}{2}L \\$
Now, we substitute the value of altitude in terms of length of the triangle in the equation of moment of inertia.
$I = \dfrac{1}{2}M{h^2} \\
\Rightarrow I = \dfrac{1}{2}M \times {\left( {\dfrac{{\sqrt 3 }}{2}L} \right)^2} \\
\therefore I = \dfrac{3}{8}M{L^2} \\$
Hence, the moment of inertia about the vertex which is parallel to the base is \[\dfrac{3}{8}M{L^2}\].

Note:While solving this problem, we should apply the parallel axis theorem in a more correct way, otherwise we will definitely get irrelevant results. Most of the students tend to make mistakes while finding the altitude in terms of length of the triangle. We must remember that a line joining one of the vertices and the centroid divides the opposite into two equal parts.