Question

Find the moment of inertia of a plate cut in shape of a right angled triangle of mass $ M $ , side $ AC = BC = a $ , about an axis perpendicular to the plane of the plate passing through midpoint of side AB

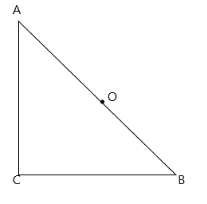
(A) $ \dfrac{{M{a^2}}}{{12}} $
(B) $ \dfrac{{M{a^2}}}{6} $
(C) $ \dfrac{{M{a^2}}}{3} $
(D) $ \dfrac{{2M{a^2}}}{3} $

Answer 1

Hint : A rectangle can be made by combining two right-angled triangles. The moment of inertia of a triangle about an axis can be said to be half the moment of inertia of a rectangle about the same axis.

Formula used: In this solution we will be using the following formula;
 $ I = \dfrac{1}{6}M{a^2} $ where $ I $ is the moment of inertia of a square plate about its centre axis perpendicular to the plane of the plate, $ M $ is the mass of the plate, and $ a $ is the length of the sides.

Complete step by step answer

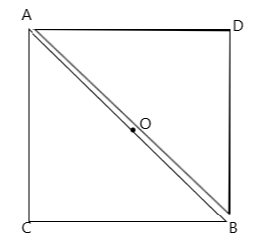
To find the moment of inertia of the triangular plate, let us join to it an imaginary triangular plate ABD of the same sides as shown in the figure. The combined structure gives a square, since sides AC and BC are equal. We have a square ACBD
Now, the moment of inertia of a square plate about its centre axis perpendicular to the plate is given as
 $ I = \dfrac{1}{6}M{a^2} $ where $ M $ is the mass of the plate, and $ a $ is the length of the sides.
Now, the mass of the triangular plate is $ M $ , then the mass of the square plate must be $ 2M $ .
Then moment of inertia of the square is
 $ I = \dfrac{1}{6}2M{a^2} = \dfrac{1}{3}M{a^2} $
Then, since, it’s about the same axis then the moment of inertia of the triangular plate is
 $ {I_t} = \dfrac{1}{2} \times \dfrac{1}{3}M{a^2} $
 $ \Rightarrow {I_t} = \dfrac{1}{6}M{a^2} $
Hence, the correct answer is option B.

Note
For clarity, the moment of inertia of the triangular plate is simply half of the square because moment of inertial can be added as
 $ {I_{ABC}} = {I_{ACBD}} - {I_{ABD}} $ where $ {I_{ABC}} $ , $ {I_{ACBD}} $ , and $ {I_{ABD}} $ is moment of inertia of triangle ABC, square ACBD and triangle ABD respectively.
Now, since we added an imaginary plate identical to original plate, then
 $ {I_{ABD}} = {I_{ABC}} = {I_t} $
Hence,
 $ {I_t} = {I_{ACBD}} - {I_t} $
By collecting like terms
 $ 2{I_t} = {I_{ACBD}} $
 $ \Rightarrow {I_t} = \dfrac{{{I_{ACBD}}}}{2} $