Question

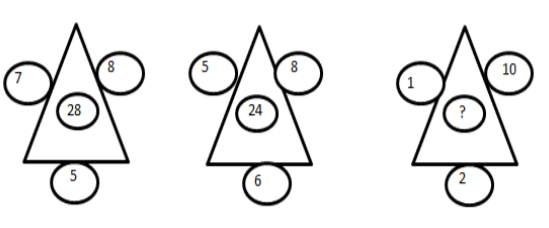
Find the missing number if same rule is applied din all three figures.
 

A.1\[\]
B.0\[\]
C.2\[\]
D.3\[\]

Answer 1

Hint: If we observe the options for the unknown in the third triangle we see that they are small. So we need to guess a rule such that the arithmetic operations involving the three numbers outside the triangle will include division or subtraction to reach the small number inside.

Complete step by step answer:
We see that we are given in the three triangles. There are four numbers in each triangle three outside the triangle and one inside the triangles. We know from the question that the four numbers in each triangle are related to each other by the same relationship.
We use the basic arithmetic operation like addition, subtraction, multiplication or division among the numbers at outside the triangles to reach the number inside the triangle.\[\]
 We are asked to find the number inside the third triangle from left. We observe the options 1,0,2,3. All of the numbers in the options are small ,so the result after we do some arithmetic operation among the numbers 1,10,2 will also be small .So one of the operations must be subtraction or division. Let us observe the first and second triangle. \[\]
We see that there are 3 numbers near the sides of the first triangle 7, 8, 5 and the number 28 is inside the triangle. If we add up the number it will be 20 which is not 28. 28 can be reached with $7\times 4=28$. We can make the rule $7\times \left( 8-5+1 \right)=28$ and we proceed to the next second triangle. \[\]
We see the numbers that are at the sides are 5,8,6 and 24 are inside it. If we go by the same rule we get $5\times \left( 8-6+1 \right)=5\times 3=15$ which is not 24, the number inside. So the rule is not correct.\[\]
If we multiply the three numbers in the first triangle we get $7\times 8\times 5=280$ which we can divide by 10 and reach 28. If we follow the same rule in the second triangle we have $\dfrac{5\times 8\times 6}{10}=\dfrac{240}{10}=24$. Now if we apply the same rule in the third triangle we have $\dfrac{2\times 1\times 10}{10}=2$.

So, the correct answer is “Option C”.

Note: The problems of this type needs guess work. If we cannot build a relation with numbers outside the triangle we may also square or cube them or divide all of them by 2 to reach the number inside.