
How do you find the missing coordinate given one point A (2, 8) and the mid – point M (5, 4)?
Answer
454.5k+ views
Hint: Assume the point whose coordinates we need to find as
Complete step by step answer:
Here we have been provided with the coordinates of a point A and the coordinates of a mid – point M. we are asked to find the coordinates of the point such that M will be the mid – point of the line segment AB. We need to apply the mid – point formula to solve the question. Let us draw a diagram of the given situation.
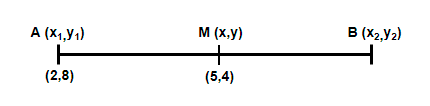
Now, assuming the coordinates of coordinates of A as
We know that the coordinates of the mid – point of a line segment according to the above assumed coordinates is given by the mid – point formula. The x – coordinate is given as
(i) For x – coordinate we have,
Substituting the given values in the above relation we get,
By cross – multiplication we get,
(i) For y – coordinate we have,
Substituting the given values in the above relation we get,
By cross – multiplication we get,
Hence the required coordinates of the point B is B (8, 6).
Note: Note that the mid – point formula is a special case of the section formula in which a point divides the line segment joining two points internally in the ratio
Complete step by step answer:
Here we have been provided with the coordinates of a point A and the coordinates of a mid – point M. we are asked to find the coordinates of the point such that M will be the mid – point of the line segment AB. We need to apply the mid – point formula to solve the question. Let us draw a diagram of the given situation.

Now, assuming the coordinates of coordinates of A as
We know that the coordinates of the mid – point of a line segment according to the above assumed coordinates is given by the mid – point formula. The x – coordinate is given as
(i) For x – coordinate we have,
Substituting the given values in the above relation we get,
By cross – multiplication we get,
(i) For y – coordinate we have,
Substituting the given values in the above relation we get,
By cross – multiplication we get,
Hence the required coordinates of the point B is B (8, 6).
Note: Note that the mid – point formula is a special case of the section formula in which a point divides the line segment joining two points internally in the ratio
Latest Vedantu courses for you
Grade 11 Science PCM | CBSE | SCHOOL | English
CBSE (2025-26)
School Full course for CBSE students
₹41,848 per year
Recently Updated Pages
Master Class 11 Physics: Engaging Questions & Answers for Success

Master Class 11 Chemistry: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Class 11 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Trending doubts
Explain why it is said like that Mock drill is use class 11 social science CBSE

Which of the following blood vessels in the circulatory class 11 biology CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Which of the following is nitrogenfixing algae a Nostoc class 11 biology CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




