Question

Find the minimum length in cm and correct the nearest whole number of the tin metal sheet required to make a hollow and closed cylindrical box of diameter $20cm$ and height$35cm$. Given that the width of the metal sheet is $1m.$Also, find the cost of sheet at the rate of Rs.$56$per m. Find the area of metal sheet required, if $10\% $of it is wasted in cutting, overlapping, etc.
A. $18cm\,\,and\,Rs.15.68;\,3,111c{m^2}$
B. $28cm\,and\,Rs.15.68;3,111c{m^2}$
C. $38cm\,\,and\,Rs.15.68;3,111c{m^2}$
D. $48cm\,and\,\,Rs.15.68;3,111c{m^2}$

Answer 1

Hint: A cylinder is a closed solid shape that has two balanced base connected by a curved surface. And the formula of total surface of cylinder $2\pi r(r + h)$

Complete step-by-step answer:

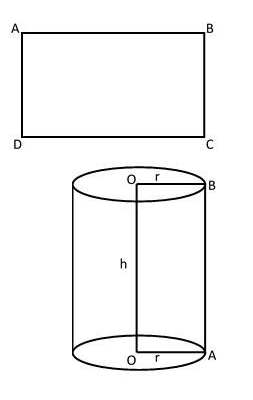
Diameter (d) $ = 20cm$
Radius(r) $ = \dfrac{d}{2}$
Radius(r)$\dfrac{{20}}{2}cm$
Radius (r)$ = 10cm$
Now, we will calculate the total surface area of the cylinder.
So, total surface area of cylinder (TSA)$ = 2\pi r(r + h)$
Here (r)$ = 10cm$
(h) $ = 35cm$
Then, we will put the values of r and h in the above formula, we will get
TSA of cylinder $ = 2\pi r(r + h)$
TSA of cylinder $ = 2 \times \pi \times 10(10 + 35)$
TSA of cylinder $ = 2 \times \pi \times 10 \times 45$
TSA of cylinder $ = \dfrac{{2 \times 22}}{7} \times 10 \times 45$
TSA of cylinder $ = \dfrac{{440 \times 45}}{7}$
TSA of cylinder $ = \dfrac{{19800}}{7}$
TSA of cylinder $ = 282.57c{m^2}$
We will convert the value of the total surface of the cylinder into m. So,
$1m = 100cm$
$1{m^2} = 10000c{m^2}$
Then,
TSA of cylinder $ = 282.57 \times \dfrac{1}{{10000}}{m^2}$
TSA of cylinder $ = 0.282857{m^2}$
TSA of cylinder $ = 0.282{m^2}$
Then, the cost of sheet at rate$56p/m$, so, we will multiply TSA of cylinder by rate
Cost of sheet $ = 0.282 \times 56$
Cost of sheet $ = $₹5.792
Cost of sheet $ = $₹$15.8$
Now, length of sheet $ = \dfrac{{total\,\,area\,\,of\,\,sheet}}{{width\,\,of\,\,sheet}}$
Length of sheet $ = \dfrac{{0.282}}{1}$
Length of sheet $28.2Cm$
Now, Area of metal sheet is $10\% $ of it is wasted in cutting, then
Area of metal sheet required $ = area\,\,of\,\,sheet + 10\% \,of\,\,area\,\,of\,\,sheet$
Area of metal sheet required $ = 2828.57 + 10\% \,\,of\,\,2828.57$
Area of metal sheet required $ = 2828.57 + \dfrac{{10}}{{100}} \times 2828.57$
Area of metal sheet required $ = 2828.57 + 282.857$
Area of metal sheet required $ = 3,111.427c{m^3}$
Area of metal sheet required $ = 3,111.43c{m^2}$
So, the correct answer is “Option B”.

Note: In these types of questions, students must know that the wasted or overlapping of sheets will be added in the area of the sheet to get the answer.