Question

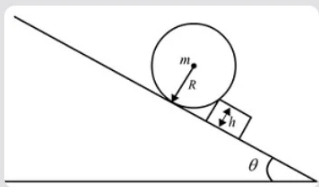
Find the minimum height of the obstacle so that the sphere can stay in equilibrium.

A. $\dfrac{R}{{1 + \cos \theta }}$
B. $\dfrac{R}{{1 + \sin \theta }}$
C. $R(1 - \sin \theta )$
D. $R(1 - \cos \theta )$

Answer 1

Hint:The sphere is on an inclined plane obstructed by an obstacle. The weight of the sphere acts downwards. The force due to weight is given as, $W = mg$. The normal force provided by the surface acts upwards and perpendicular to the sphere. The normal force is equal and opposite to the gravitational force acting on the sphere. This normal force is the force applied by the surface which prevents the sphere from falling. The normal force makes an angle with the inclined surface.


Complete step by step solution:

Given,
The mass of the sphere is $m$.
The radius of the sphere is $R$.
The height of the obstacle is $h$.
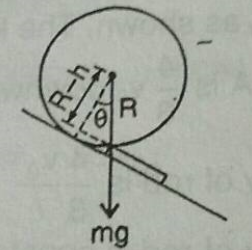
The distance from the center of sphere to the obstacle edge is $R - h$.
The angle subtended by the normal force with the obstacle is $\theta $.
The equilibrium is because of the action of weight and the normal reaction provided by the surface of the inclined plane.
The minimum height can be calculated by taking cosine of the angle as,
$\cos \theta = \dfrac{{base}}{{hypotenuse}} = \dfrac{{R - h}}{R}$ …… (1)

Simplifying the equation (1) we get,
$\begin{array}{l}\cos \theta = \dfrac{{R - h}}{R}\\ \Rightarrow R\cos \theta = R - h\\ \Rightarrow h = R - R\cos \theta \\ \Rightarrow h = R(1 - \cos \theta )\end{array}$

Hence the correct answer is (D).

Note:The students have to apply the concept of normal reaction when a body is on an inclined plane or surface. In this case, the obstacle prevents the sphere from falling. The equilibrium is because of the line of action of weight and the normal reaction provided by the surface. The normal force applied by the surface prevents the sphere from falling.