
Find the midpoint of the, line segment joining the points P(3,4) and Q(5,-2)
Answer
587.7k+ views
Hint: Midpoint is the middle point of the line segment that divides it into two equal parts. Thus, it can be said midpoint is half of the sum of initial and final points of line segment.In the following figure, PQ is a line segment in XY plane ( as the mentioned coordinates lie on the x and y axis) and M is its middle point.
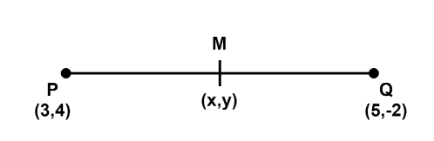
Complete step-by-step answer:
In geometry, the midpoint is the middle point of a line segment. It is equidistant from both endpoints, and it is the centroid both of the segment and of the endpoints. It bisects the segment.
Just as finding the midpoint is often required in geometry, so is finding the distance between two points. The distance between two points on a horizontal or vertical line is easy to calculate, but the process becomes more difficult if the points are not aligned as such. This is often the case when dealing with sides of a triangle. In some geometrical cases, we wish to inscribe a triangle inside another triangle, where the vertices of the inscribed triangle lie on the midpoint of the original triangle. The midpoint calculator is extremely useful in such cases.
Let coordinates of P be (x1,y1) , Q be (x2,y2) and midpoint M be (x, y). Therefore,
x1 = 3 x2= 5
y1= 4 y2= -2
As middle point is half the sum of initial and final points of the line segment, for respective axis it can be written as:
\[x = \dfrac{{{x_1} + {x_2}}}{2};y = \dfrac{{{y_1} + {y_2}}}{2}\]
Substituting the values, we get:
$ x = \dfrac{{3 + 5}}{2} $ $ y = \dfrac{{4 + ( - 2)}}{2} $
$ x = \dfrac{8}{2} $ $ y = \dfrac{2}{2} $
$ x = 4 $ $ y = 1 $
\[M = \left( {x,y} \right) = \left( {4,1} \right)\]
Therefore coordinates of the midpoint of the line segment joining P(3,4) and Q(5,-2) are (4,1).
Note: When the coordinates of points in the XY plane are mentioned, the point on the x-axis is always written before Y.
Eg: P (3, 4) → 3 is x coordinate and 4 is y coordinate.
x - axis and y-axis can be called abscissa and ordinate as well.
Enclose negative terms in brackets to avoid calculation mistakes.

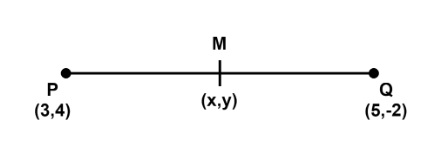
Complete step-by-step answer:
In geometry, the midpoint is the middle point of a line segment. It is equidistant from both endpoints, and it is the centroid both of the segment and of the endpoints. It bisects the segment.
Just as finding the midpoint is often required in geometry, so is finding the distance between two points. The distance between two points on a horizontal or vertical line is easy to calculate, but the process becomes more difficult if the points are not aligned as such. This is often the case when dealing with sides of a triangle. In some geometrical cases, we wish to inscribe a triangle inside another triangle, where the vertices of the inscribed triangle lie on the midpoint of the original triangle. The midpoint calculator is extremely useful in such cases.

Let coordinates of P be (x1,y1) , Q be (x2,y2) and midpoint M be (x, y). Therefore,
x1 = 3 x2= 5
y1= 4 y2= -2
As middle point is half the sum of initial and final points of the line segment, for respective axis it can be written as:
\[x = \dfrac{{{x_1} + {x_2}}}{2};y = \dfrac{{{y_1} + {y_2}}}{2}\]
Substituting the values, we get:
$ x = \dfrac{{3 + 5}}{2} $ $ y = \dfrac{{4 + ( - 2)}}{2} $
$ x = \dfrac{8}{2} $ $ y = \dfrac{2}{2} $
$ x = 4 $ $ y = 1 $
\[M = \left( {x,y} \right) = \left( {4,1} \right)\]
Therefore coordinates of the midpoint of the line segment joining P(3,4) and Q(5,-2) are (4,1).
Note: When the coordinates of points in the XY plane are mentioned, the point on the x-axis is always written before Y.
Eg: P (3, 4) → 3 is x coordinate and 4 is y coordinate.
x - axis and y-axis can be called abscissa and ordinate as well.
Enclose negative terms in brackets to avoid calculation mistakes.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




