Question

How do you find the midpoint of $\left( -5,4 \right)$ and $\left( 3,2 \right)$ ?

Answer 1

Hint: Take the two given points as $'A'$ and $'B'$ respectively. Let their midpoint be $'C'$. For the ‘x’- coordinate of the midpoint add the ‘x’- coordinates of the two given points and divide them by ‘2’ i.e. $\dfrac{{{x}_{1}}+{{x}_{2}}}{2}$ . Similarly for the ‘y’- coordinate of the midpoint add the ‘y’- coordinates of the two given points and divide them by ‘2’ i.e. $\dfrac{{{y}_{1}}+{{y}_{2}}}{2}$.

Complete step by step answer:
Midpoint of a line segment: If we have a line segment $\overrightarrow{AB}$ with the coordinates of $A\left( {{x}_{1}},{{y}_{1}} \right)$ and $B\left( {{x}_{2}},{{y}_{2}} \right)$ and $'C'$ is the midpoint of $'A'$ and $'B'$, then
The ‘x’- coordinate of the midpoint $'C'$$=\dfrac{{{x}_{1}}+{{x}_{2}}}{2}$
The ‘y’- coordinate of the midpoint $'C'$$=\dfrac{{{y}_{1}}+{{y}_{2}}}{2}$
So, the coordinates of $C\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$
Now considering the points given in the question, we have
$A\left( -5,4 \right)$
So, ${{x}_{1}}=-5$, ${{y}_{1}}=4$
And $B\left( 3,2 \right)$
So, ${{x}_{2}}=3$, ${{y}_{2}}=2$
Let the midpoint of $'A'$ and $'B'$ be $'C'$ as shown below,

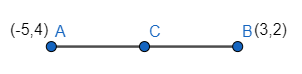
Then we get the ‘x’- coordinate of the midpoint $'C'$$=\dfrac{-5+3}{2}=\dfrac{-2}{2}=-1$ .
The ‘y’- coordinate of the midpoint $'C'$$=\dfrac{4+2}{2}=\dfrac{6}{2}=3$ .
Hence, $C\left( -1,3 \right)$ .
This is the required solution for the given question.

Note: The midpoint is halfway between the two end points. So, it’s ‘x’- value is halfway between the two ‘x’- values. Similarly, it’s ‘y’- value is halfway between the two ‘y’- values. So for the calculation of ‘x’- coordinate of the midpoint both the ‘x’- coordinates are added and divided by ‘2’ and for ‘y’- coordinate of the midpoint both the ‘y’- coordinates are added and divided by ‘2’. The final midpoint value should be written in the format $C\left( x,y \right)$.