Question

Find the measure of the third angle of triangles whose two angles are given below
(i) \[38^\circ, 100^\circ\] (ii) \[116^\circ, 30^\circ\] (iii) \[40^\circ, 80^\circ\]

Answer 1

Hint: The sum of all angles of a triangle is equal to \[180^\circ\].
Consider the triangle with angles \[a\], \[b\] and \[c\] respectively.

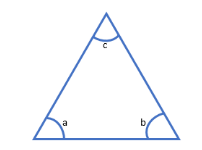
From the figure, it follows \[a+b+c = 180^\circ\].

Complete step-by-step answer:
The two angles of the triangle are given as \[38^\circ\] and \[100^\circ\].
Since the sum of the angles of the triangles is equal to \[180^\circ\], the third angle is given by subtracting the sum of the other two angles from \[180^\circ\].
Therefore, the third angle of the triangle is,
\[180^\circ-(38^\circ+100^\circ) = 180^\circ-138^\circ = 42^\circ \]
The angles are given as \[116^\circ\] and \[30^\circ\].
Since the sum of the angles of the triangles is equal to \[180^\circ\],, the third angle is given by subtracting the sum of the other two angles from \[180^\circ\].
Therefore, the third angle of the triangle is,
\[180^\circ-(116^\circ+30^\circ) = 180^\circ-146^\circ = 34^\circ \]
The angles are given as \[40^\circ\] and \[80^\circ\],.
Since the sum of the angles of the triangles is equal to \[180^\circ\],, the third angle is given by subtracting the sum of the other two angles from \[180^\circ\].
Therefore, the third angle of the triangle is,
\[180^\circ-(40^\circ+80^\circ) = 180^\circ-120^\circ = 60^\circ \]

Note: Any exterior angle of a triangle can be determined using this property of the triangle. In the case of a right angled triangle, one angle is equal to \[90^\circ\] and so the other two angles sum up to \[90^\circ\].
In the case of an equilateral triangle, each of the three angles of the triangle is \[60^\circ\] such that their sum is \[180^\circ\].