Question

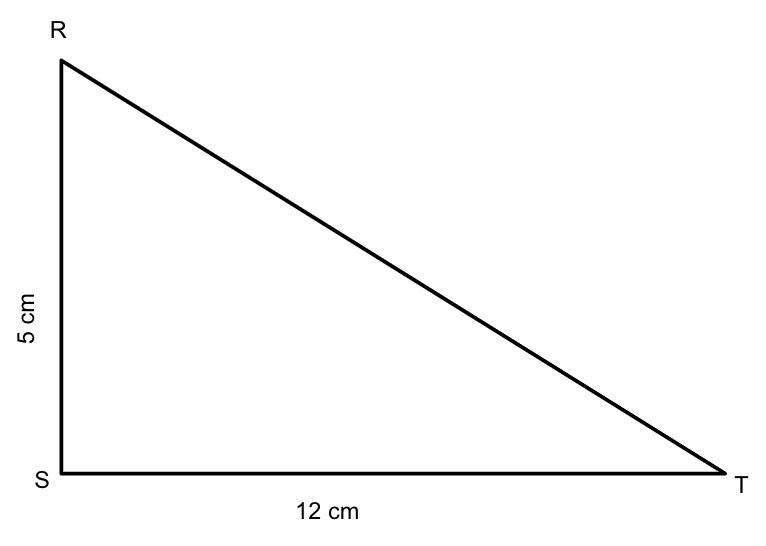
Find the measure of RT.

Answer 1

Hint: First, we will assume that measure of RT is \[x\]. Then use the Pythagorean theorem on the sides of triangle, \[{h^2} = {a^2} + {b^2}\], where \[h\] is the hypotenuse, \[a\] is the height and \[b\] is the base of the triangle. Then we will simplify the equation to find the value of \[x\].

Complete step by step answer:

We are given that the measure of ST is 5 cm and ST is 12 cm.
Let us assume that measure of RT is \[x\].
First, we will draw the triangle where the hypotenuse is \[x\] cm, perpendicular is 5 cm and the base is 12 cm.

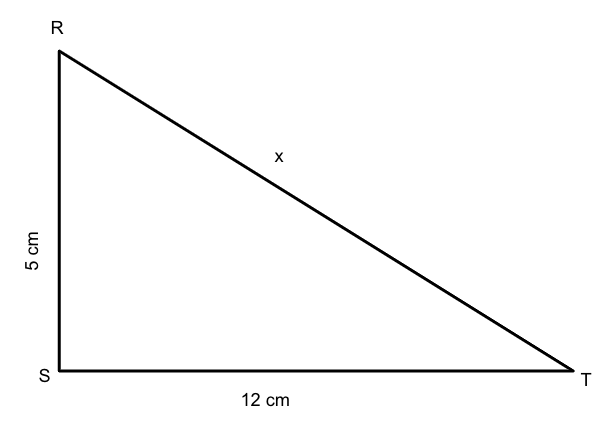
We know that the Pythagorean theorem \[{h^2} = {a^2} + {b^2}\], where \[h\] is the hypotenuse, \[a\] is the height and \[b\] is the base of the triangle.
Using the Pythagorean theorem on the given sides of the right-angled triangle RST and then simplify, we get
\[
   \Rightarrow {x^2} = {5^2} + {12^2} \\
   \Rightarrow {x^2} = 25 + 144 \\
   \Rightarrow {x^2} = 169 \\
 \]
Taking square root in the above equation, we get
\[
   \Rightarrow x = \pm \sqrt {169} \\
   \Rightarrow x = \pm 13 \\
 \]
Since the side of a right-angled triangle cannot be negative, we will discard \[x = - 13\].
Thus, the measure of RT is 13 cm.

Note: In these types of questions, we will draw the diagram of a right-angled triangle for better understanding. In this question, first of all, note that the equation is solved only using the Pythagorean theorem to find the value of \[x\]. Also, some students end the question right after calculating the value of \[x\] and forget to write the unit in the final answer.