Question

Find the measure of each angle of an equilateral triangle.

Answer 1

Hint – In this question consider one angle of an equilateral angle be a variable and use the property of an equilateral triangle than its interior angles are all equal. Apply the angle sum property to get the answer.

Complete step-by-step answer:

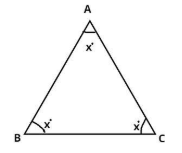
Consider the equilateral triangle ABC as shown in figure.
Now as we know that in equilateral triangles all angles are equal.
So let,
$\angle A = \angle B = \angle C = {x^ \circ }$ as shown in figure.
Now as we know that in a triangle the sum of all angles is equal to 180 degree.
$ \Rightarrow \angle A + \angle B + \angle C = {180^ \circ }$
Now substitute the values in above equation we have,
$ \Rightarrow x + x + x = {180^ \circ }$
$ \Rightarrow 3x = {180^ \circ }$
Now divide by 3 we have,
$ \Rightarrow x = \dfrac{{{{180}^ \circ }}}{3} = {60^ \circ }$
So each angle of the equilateral triangle = $60^0$.
So this the required measure of each angle.
So this is the required answer.

Note – An equilateral triangle is one such that all the sides of it are equal, the reason behind all the angles of an equilateral triangle being equal is that the angles opposite to equal sides are always equal. All internal angles of an equilateral triangle are congruent to each other and are each of ${60^0}$.