Question

Find the maximum and minimum values of ${\sin ^{ - 1}}x + {\text{ta}}{{\text{n}}^{ - 1}}x.$

Answer 1

Hint: Here in these types of problems, where we are asked to find the maximum or minimum value of the given function, we need to see whether the graph is increasing or decreasing. If it is fully increasing or decreasing for the domain. Then the maximum and minimum values of the function will be at the maximum and minimum values of the domain.

Complete step-by-step answer:
Here we are given to find the maximum and minimum values of the function which is ${\sin ^{ - 1}}x + {\text{ta}}{{\text{n}}^{ - 1}}x.$
We must know that the domain of ${\sin ^{ - 1}}x = \left[ { - 1,1} \right]$ and of ${\text{ta}}{{\text{n}}^{ - 1}}x = \left( { - \infty ,\infty } \right)$
So if we need to find the common domain which means that the values that can be taken for the variable $x$ for both ${\sin ^{ - 1}}x{\text{ and ta}}{{\text{n}}^{ - 1}}x$ at the same time. So the common domain will be $\left[ { - 1,1} \right]$ because the value above $1$ and below $ - 1$ will not satisfy the function ${\sin ^{ - 1}}x$
So for the common domain $\left[ { - 1,1} \right]$ we need to find the maximum value of ${\sin ^{ - 1}}x + {\text{ta}}{{\text{n}}^{ - 1}}x.$
We need to plot their graph as by seeing the graphs of both the functions we can come to know if they are increasing/decreasing or neither strictly increasing nor strictly decreasing.
Graph of ${\sin ^{ - 1}}x$

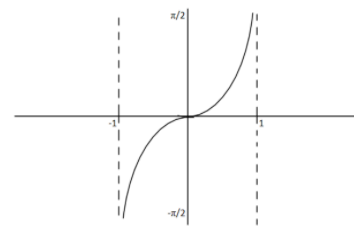
From the graph of ${\sin ^{ - 1}}x$ we can notice that it is strictly increasing in its domain which is $\left[ { - 1,1} \right]$
Graph of ${\text{ta}}{{\text{n}}^{ - 1}}x$

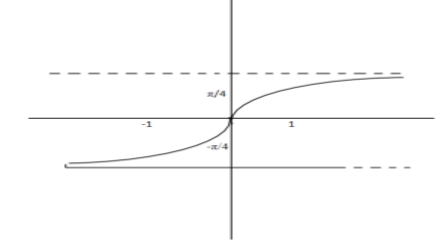
This graph also, as we notice, is strictly increasing for all the values that come in its domain.
Hence we can say that the function ${\sin ^{ - 1}}x + {\text{ta}}{{\text{n}}^{ - 1}}x$ is strictly an increasing function.
Whenever the function is strictly increasing in the domain then we must know that the minimum and maximum values of the domain gives us the minimum and maximum values of the function.
Hence minimum value occurs at $x = - 1$
Minimum value of ${\sin ^{ - 1}}x + {\text{ta}}{{\text{n}}^{ - 1}}x$$ = {\sin ^{ - 1}}\left( { - 1} \right) + {\text{ta}}{{\text{n}}^{ - 1}}\left( { - 1} \right)$
Minimum value$ = - \dfrac{\pi }{2} - \dfrac{\pi }{4} = \dfrac{{ - 2\pi - \pi }}{4} = - \dfrac{{3\pi }}{4}$
Maximum value will occur at $x = 1$
Maximum value of ${\sin ^{ - 1}}x + {\text{ta}}{{\text{n}}^{ - 1}}x$$ = {\sin ^{ - 1}}\left( 1 \right) + {\text{ta}}{{\text{n}}^{ - 1}}\left( 1 \right)$
Maximum value$ = \dfrac{\pi }{2} + \dfrac{\pi }{4} = \dfrac{{2\pi + \pi }}{4} = \dfrac{{3\pi }}{4}$
Hence we get that:
Minimum value$ = - \dfrac{{3\pi }}{4}$
Maximum value$ = \dfrac{{3\pi }}{4}$

Note: Here in these types of problems students can also proceed by using the differentiation of the function and equate it to zero to find whether the function is increasing or not but it can take some time. So we must always try to plot the graph first as it makes the solution clearer.