Question

Find the locus of the points of intersection of tangents drawn at the ends of all chords normal to the parabola \[{{y}^{2}}=8\left( x-1 \right)\].

Answer 1

Hint: Assume \[x-1=X\] and \[y=Y\] and solve the whole question using the result of the standard parabola \[{{y}^{2}}=4ax\]. Later, replace \[X\] and \[Y\] with their actual values.

Complete step-by-step answer:

We are given a parabola \[{{y}^{2}}=8\left( x-1 \right)\]. We have to find the locus of the points of intersection of tangents drawn at the ends of the chords normal to the given parabola.

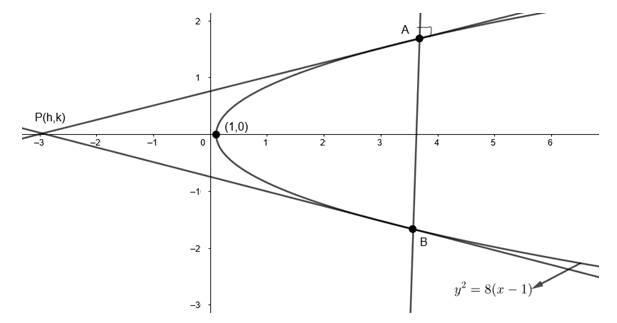
Let \[P\left( h,k \right)\] be the point of intersection of tangents and \[AB\] be the normal chord.

We are given parabola, \[{{y}^{2}}=8\left( x-1 \right)\]

Let\[y=Y\] and \[x-1=X\] to get a general parabola of the form \[{{y}^{2}}=4ax\].

So now, we get a parabola \[{{Y}^{2}}=8X\]

Now, we know that for any parabola of the form \[{{y}^{2}}=4ax\], equation of normal is
\[y=mx-2am-a{{m}^{3}}\]

For the given parabola, \[4a=8\]
So, we get \[a=2\]

So, our equation for normal to the parabola, \[{{Y}^{2}}=8X\] which is \[AB\] which is given by
\[Y=mX-2am-a{{m}^{3}}\]

Since, \[a=2\], we get \[Y=mX-4m-2{{m}^{3}}....\left( i \right)\]

As \[P\left( h,k \right)\] is the point of intersection of tangents at the ends of normal chord \[AB\], therefore \[AB\] would be a chord of contact with respect to a point \[\left( h,k \right)\].

We know that equation of chord of contact of tangents drawn from a point \[P\left( x,y \right)\] of the parabola \[{{y}^{2}}=4ax\] is \[y{{y}_{1}}=2a\left( x+{{x}_{1}} \right)\]

Therefore, we get the equation of chord of contact of the point \[\left( h,k \right)\] of the parabola \[{{Y}^{2}}=8X\] is:
\[Yk=2\times 2\left( X+h \right)\]

Here, we get \[Yk=4X+4h....\left( ii \right)\]

Since we know that both equations \[\left( i \right)\]and \[\left( ii \right)\] are the equation of chord \[AB\].

Therefore, now we will compare the coefficients of \[X\] and \[Y\] and the constant of the equation \[\left( i \right)\]and \[\left( ii \right)\].

Hence we get, \[\dfrac{1}{k}=\dfrac{m}{4}=\dfrac{-\left( 4m+2{{m}^{3}} \right)}{4h}\]

Taking \[\dfrac{1}{k}=\dfrac{m}{4}\]
We get, \[m=\dfrac{4}{k}\]

Taking \[\dfrac{1}{k}=\dfrac{-\left( 4m+2{{m}^{3}} \right)}{4h}\]
Now we will put the value of \[m=\dfrac{4}{k}\].

Hence, we get \[\dfrac{1}{k}=\dfrac{-\left( 4\left( \dfrac{4}{k} \right)+2{{\left( \dfrac{4}{k} \right)}^{3}} \right)}{4h}\]

By cross multiplying above equation,
We get, \[4h=-k\left[ \dfrac{16}{k}+\dfrac{128}{{{k}^{3}}} \right]\]
\[\Rightarrow 4h=-k\left[ \dfrac{16{{k}^{2}}+128}{{{k}^{3}}} \right]\]

By cross multiplying above equation and canceling \[4\] from both sides we get,
\[h{{k}^{2}}=-4{{k}^{2}}-32\]
Or, \[{{k}^{2}}\left( h+4 \right)+32=0\]

To find the locus, replace \[h\] by \[X\] and \[k\] by \[Y\]
So, we get \[{{Y}^{2}}\left( X+4 \right)+32=0\]

As we had assumed that \[Y=y\]and \[X=x-1\], therefore replacing \[X\] and \[Y\] with their actual values,
We get, \[{{y}^{2}}\left( x-1+4 \right)+32=0\]
\[{{y}^{2}}\left( x+3 \right)+32=0\]

Therefore, the locus of points of intersection of tangents at the ends of the normal chord of the parabola \[{{y}^{2}}=8\left( x-1 \right)\] is \[{{y}^{2}}\left( x+3 \right)+32=0\]

Note: Students must note that general equations of normals, tangents, etc are given for parabola for the form \[{{y}^{2}}=4ax\] and for any variations in the general form of the parabola will also vary the equations of normals, tangents, etc. Always remember to replace \[X\] and \[Y\] with their actual values before assumption like in this question \[X=x-1\] and \[Y=y\]