Question

Find the locus of the middle points of chords of the parabola which pass through the fixed point \[\left( h,\text{ }k \right)\].

Answer 1

Hint: Write the slope point form of a line passing through points, say \[B\left( a{{t}^{2}},2at \right)\] and \[C\left( a{{u}^{2}},2au \right)\]that lies on the chord of the parabola. Then, we can substitute \[\left( h,k \right)\] in it to get the equation. Then we can use the midpoint formula to get the coordinates of the midpoint of the chord. We can find its locus by substituting the variables in the equation of the chord we had found out.

Complete step-by-step answer:

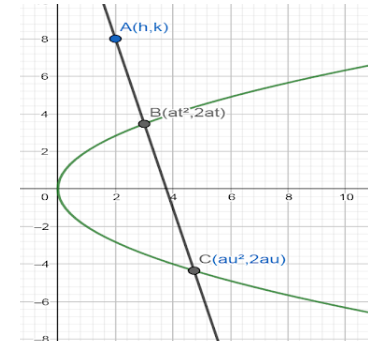
Let us consider the above picture. \[B\left( a{{t}^{2}},2at \right)\] and \[C\left( a{{u}^{2}},2au \right)\] are two variable points on a standard parabola \[{{y}^{2}}=4ax\] with parameters \[t\] and \[u\] respectively. \[A\left( h,k \right)\] is a fixed point through which our variable line passes.
We have to find the locus of mid-points of the chord \[BC\]. We can write the equation of \[BC\] using two- point form of a line which is,
$\dfrac{y-y1}{x-x1}=\dfrac{y2-y1}{x2-x1}$
So we get the equation of line \[BC\] as,
$BC:\dfrac{y-2at}{x-a{{t}^{2}}}=\dfrac{2au-2at}{a{{u}^{2}}-a{{t}^{2}}}$
Also, the point \[A\left( h,k \right)\] lies on the line \[BC\] so it must also satisfy its equation. So substituting it, we get
$\dfrac{k-2at}{h-a{{t}^{2}}}=\dfrac{2au-2at}{a{{u}^{2}}-a{{t}^{2}}}$
Cross-multiplying and further simplifying we get,
$\begin{align}
  & \left( k-2at \right)\left( u+t \right)=2\left( h-a{{t}^{2}} \right) \\
 & ku+kt-2aut-2a{{t}^{2}}=2h-2a{{t}^{2}} \\
 & ku+kt-2aut=2h \\
 & k\left( u+t \right)-2aut-2h=0...(i) \\
\end{align}$
To find the locus of the point, we consider a point with coordinates \[\left( {{x}_{1}},{{y}_{1}} \right)\], which is a general point on the locus. Since \[\left( {{x}_{1}},{{y}_{1}} \right)\] lies on the locus which is the locus of mid-points of the chord of the parabola, we can use midpoint formula and we can write that \[{{X}_{mid}}=\dfrac{{{x}_{1}}+{{x}_{2}}}{2}\] and \[{{Y}_{mid}}=\dfrac{{{y}_{1}}+{{y}_{2}}}{2}\]. Therefore, we will get the coordinates as below,
${{x}_{1}}=\left\{ \dfrac{\left( x~coordinate~of~A \right)+\left( x~coordinate~of~B \right)}{2} \right\}$
${{x}_{1}}=\left\{ \dfrac{\left( a{{t}^{2}} \right)+\left( a{{u}^{2}} \right)}{2} \right\}$
$2{{x}_{1}}=\left( a{{t}^{2}} \right)+\left( a{{u}^{2}} \right)$
$\dfrac{2{{x}_{1}}}{a}=\left\{ {{t}^{2}}+{{u}^{2}} \right\}...(ii)$
${{y}_{1}}=\left\{ \dfrac{\left( y~coordinate~of~A \right)+\left( y~coordinate~of~B \right)}{2} \right\}$
${{y}_{1}}=\left\{ \dfrac{\left( 2at \right)+\left( 2au \right)}{2} \right\}$
${{y}_{1}}=\left( at \right)+\left( au \right)$
$\dfrac{{{y}_{1}}}{a}=\left\{ t+u \right\}...(iii)$
So our next task in finding the locus is eliminating the variables from the above equations. Squaring equation \[\left( iii \right)\] and subtracting it from \[\left( ii \right)\] i.e. \[{{\left( iii \right)}^{2}}-\left( ii \right)\] gives,
${{\left( \dfrac{{{y}_{1}}}{a} \right)}^{2}}-\dfrac{2{{x}_{1}}}{a}={{\left( t+u \right)}^{2}}-\left\{ {{u}^{2}}+{{t}^{2}} \right\}$
${{\left( \dfrac{{{y}_{1}}}{a} \right)}^{2}}-\dfrac{2{{x}_{1}}}{a}=\left( {{t}^{2}}+{{u}^{2}}+2ut \right)-\left\{ {{u}^{2}}+{{t}^{2}} \right\}$
${{\left( \dfrac{{{y}_{1}}}{a} \right)}^{2}}-\dfrac{2{{x}_{1}}}{a}=2ut...(iv)$
Substituting equation \[\left( iii \right)\] and \[\left( iv \right)\] in \[\left( i \right)\],
$k\left( \dfrac{{{y}_{1}}}{a} \right)-a\left[ {{\left( \dfrac{{{y}_{1}}}{a} \right)}^{2}}-\dfrac{2{{x}_{1}}}{a} \right]-2h=0$
Multiplying the terms with a, we get
$k{{y}_{1}}-{{a}^{2}}\left[ {{\left( \dfrac{{{y}_{1}}}{a} \right)}^{2}}-\dfrac{2{{x}_{1}}}{a} \right]-2ah=0$
Simplifying the equation further, we get
$\begin{align}
  & \Rightarrow k{{y}_{1}}-{{a}^{2}}\left[ \dfrac{{{y}_{1}}^{2}}{{{a}^{2}}}-\dfrac{2{{x}_{1}}}{a} \right]-2ah=0 \\
 & \Rightarrow k{{y}_{1}}-{{a}^{2}}\left[ \dfrac{{{y}_{1}}^{2}-2a{{x}_{1}}}{{{a}^{2}}} \right]-2ah=0 \\
 & \Rightarrow k{{y}_{1}}-{{y}_{1}}^{2}+2a{{x}_{1}}-2ah=0 \\
\end{align}$
Now since \[\left( {{x}_{1}},{{y}_{1}} \right)\] are general points on our locus, we can replace \[{{x}_{1}}\] by \[x\] and \[{{y}_{1}}\] by \[y\].
$\begin{align}
  & \Rightarrow ky-{{y}^{2}}+2ax-2ah=0 \\
 & \Rightarrow -{{y}^{2}}+ky+2a\left( x-h \right)=0 \\
 & \Rightarrow {{y}^{2}}-ky-2a\left( x-h \right)=0 \\
 & \Rightarrow {{y}^{2}}=ky-2a\left( x-h \right) \\
\end{align}$
Hence, ${{y}^{2}}=ky-2a\left( x-h \right)$ is the required locus.

Note: In this question, if the student knows the equation of the chord of the parabola, then they can directly use it instead of deriving it. This will help the student save time in the exams. The student must make sure to simplify the locus and represent it in the simplest form possible.