Question

Find the locus of the middle points of chords of the parabola which are such that the normals at their extremities meet on the parabola.

Answer 1

Hint: Take two general points on the parabola and draw normal at those points. The normals should intersect at the parabola.

Complete step-by-step answer:

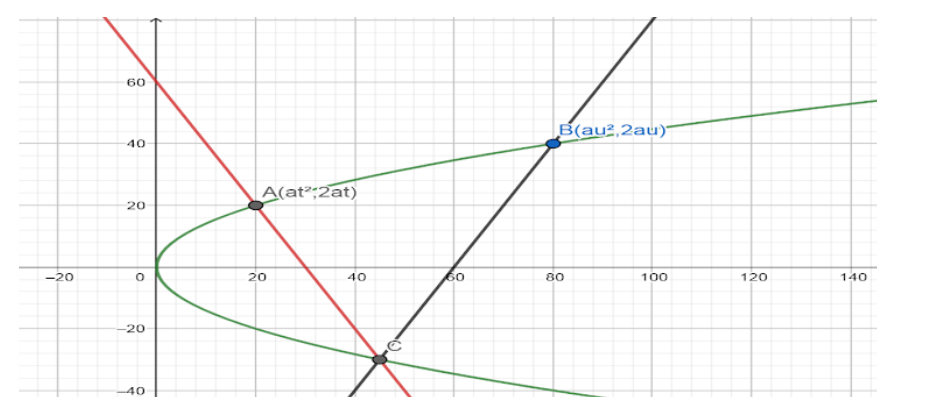
Consider the above picture. \[A\left( a{{t}^{2}},2at \right)\] and \[B\left( a{{u}^{2}},2au \right)\] are two variable points on the standard parabola \[{{y}^{2}}=4ax\] with parameters \[t\] and \[~u\] respectively.
It is given that \[AC\]and \[BC\] are normal to the parabola at points \[A\] and \[B\] respectively.
We can write equations for \[AC\] and \[BC\] using the formula for normals which is,
Normal at a point with parameter (\[t\]) is given by,
\[y+tx=2at+a{{t}^{3}}\]
So we get equations of lines\[AC\] and \[BC\]as,
\[AC:y+tx=2at+a{{t}^{3}}...(i)\]
\[BC:y+ux=2au+a{{u}^{3}}...(ii)\]
Subtracting equation \[(i)\] from \[(ii)\]i.e.\[\left( ii \right)-\left( i \right)\] we get,
\[\left( y+tx \right)-\left( y+ux \right)=\left( 2at+a{{t}^{3}} \right)-\left( 2au+a{{u}^{3}} \right)\]
\[tx-ux=2at-2au+a{{t}^{3}}-a{{u}^{3}}\]
\[(t-u)x=2a(t-u)+a({{t}^{3}}-{{u}^{3}})\]
\[(t-u)x=2a(t-u)+a(t-u)({{t}^{2}}+{{u}^{2}}+ut)\]
\[x=2a+a({{t}^{2}}+{{u}^{2}}+ut)...(iii)\]
Substituting equation \[\left( iii \right)\] in \[\left( i \right)\] we get,
\[y+t\left( 2a+a({{t}^{2}}+{{u}^{2}}+ut) \right)=2at+a{{t}^{3}}\]
\[y+2at+at({{t}^{2}}+{{u}^{2}}+ut)=2at+a{{t}^{3}}\]
\[y+2at+(a{{t}^{3}}+at{{u}^{2}}+a{{t}^{2}}u)=2at+a{{t}^{3}}\]
\[y+at{{u}^{2}}+a{{t}^{2}}u=0\]
\[y=-at{{u}^{2}}-a{{t}^{2}}u\]
$C=\left( 2a+a{{u}^{2}}+a{{t}^{2}}+aut,-a{{t}^{2}}u-a{{u}^{2}}t \right)$
We are given that point \[C\]also lies on the parabola so it also satisfies the equation \[{{y}^{2}}=4ax\]
So,
${{\left( -a{{t}^{2}}u-a{{u}^{2}}t \right)}^{2}}=4a\left( 2a+a{{u}^{2}}+a{{t}^{2}}+aut \right)$
${{\left[ \left( -aut \right)\left( t+u \right) \right]}^{2}}=4{{a}^{2}}\left( 2+{{u}^{2}}+{{t}^{2}}+ut \right)$
${{\left( -aut \right)}^{2}}{{\left( t+u \right)}^{2}}=4{{a}^{2}}\left( 2+{{u}^{2}}+{{t}^{2}}+ut \right)$
${{\left( ut \right)}^{2}}{{\left( t+u \right)}^{2}}=4\left( 2+{{u}^{2}}+{{t}^{2}}+ut \right)...(iv)$
To find the locus of a point, we consider a point with coordinates\[\left( h,k \right)\], which is a general point on the locus.
Since they lie on the locus it is the midpoint of our variable chord\[AB\].
So using the mid-point formula which is,
Xmid=\[\dfrac{x1+x2}{2}\]
ymid= \[\dfrac{y1+y2}{2}\]
We write,
$\begin{align}
  & h=\left\{ \dfrac{\left( x~coordinate~of~A \right)+\left( x~coordinate~of~B \right)}{2} \right\} \\
 & k=\left\{ \dfrac{\left( x~coordinate~of~A \right)+\left( x~coordinate~of~B \right)}{2} \right\} \\
\end{align}$
And,
$h=\left\{ \dfrac{\left( \text{a}{{\text{t}}^{2}} \right)+\left( a{{u}^{2}} \right)}{2} \right\}$
$2h=\left( \text{a}{{\text{t}}^{2}} \right)+\left( a{{u}^{2}} \right)$
$\dfrac{2h}{a}=\left\{ {{\text{t}}^{2}}+{{u}^{2}} \right\}...(v)$
$k=\left\{ \dfrac{\left( 2at \right)+\left( 2au \right)}{2} \right\}$
$k=\left( at \right)+\left( au \right)$
$\dfrac{k}{a}=\left\{ t+u \right\}...(vi)$
So our next task in finding the locus is eliminating the variables from the above equations.
Squaring equation\[\left( vi \right)\]and subtracting it from \[\left( v \right)\] i.e. \[{{\left( vi \right)}^{2}}-\left( v \right)\]
Which gives,
${{\left( \dfrac{k}{a} \right)}^{2}}-\dfrac{2h}{a}={{\left( t+u \right)}^{2}}-\left\{ {{\text{t}}^{2}}+{{u}^{2}} \right\}$
${{\left( \dfrac{k}{a} \right)}^{2}}-\dfrac{2h}{a}=\left( {{t}^{2}}+{{u}^{2}}+2ut \right)-\left\{ {{\text{t}}^{2}}+{{u}^{2}} \right\}$
${{\left( \dfrac{k}{a} \right)}^{2}}-\dfrac{2h}{a}=2ut...(vii)$
Substituting equations \[\left( v \right),\left( vi \right),\left( vii \right)\]in\[\left( iv \right)\]we get,
${{\left( \dfrac{{{\left( \dfrac{k}{a} \right)}^{2}}-\dfrac{2h}{a}}{2} \right)}^{2}}{{\left( \dfrac{k}{a} \right)}^{2}}=4\left( 2+\left( \dfrac{2h}{a} \right)+\left( \dfrac{{{\left( \dfrac{k}{a} \right)}^{2}}-\dfrac{2h}{a}}{2} \right) \right)$
\[{{\left( {{\left( \dfrac{k}{a} \right)}^{3}}-\dfrac{2h}{a}\left( \dfrac{k}{a} \right) \right)}^{2}}=16\left( 2+\left( \dfrac{2h}{a} \right)+\left( \dfrac{{{\left( \dfrac{k}{a} \right)}^{2}}-\dfrac{2h}{a}}{2} \right) \right)\]
\[{{\left( {{\left( \dfrac{k}{a} \right)}^{2}}-\dfrac{2h}{a} \right)}^{2}}{{\left( \dfrac{k}{a} \right)}^{2}}=16\left( 2+\left( \dfrac{2h}{a} \right)+\left( \dfrac{{{\left( \dfrac{k}{a} \right)}^{2}}-\dfrac{2h}{a}}{2} \right) \right)\]
\[{{\left( {{\left( \dfrac{k}{a} \right)}^{3}}-\dfrac{2h}{a}\left( \dfrac{k}{a} \right) \right)}^{2}}=16\left( 2+\left( \dfrac{2h}{a} \right)+\dfrac{1}{2}{{\left( \dfrac{k}{a} \right)}^{2}}-\dfrac{h}{a} \right)\]
\[{{\left( {{\left( \dfrac{k}{a} \right)}^{3}}-\dfrac{2hk}{{{a}^{2}}} \right)}^{2}}=16\left( 2+\dfrac{h}{a}+\dfrac{1}{2}{{\left( \dfrac{k}{a} \right)}^{2}} \right)\]
Now since \[\left( h,k \right)\]are general points on our locus we can replace \[h\] by \[x\] and \[k\] by \[y\].
\[{{\left( {{\left( \dfrac{y}{a} \right)}^{3}}-\dfrac{2xy}{{{a}^{2}}} \right)}^{2}}=16\left( 2+\dfrac{x}{a}+\dfrac{1}{2}{{\left( \dfrac{y}{a} \right)}^{2}} \right)\]
This is the required locus.

Note: Students have to think carefully while deciding which is the variable before eliminating. In this question students might eliminate \[a\] which will give them the wrong answer. Also they may use their different techniques to eliminate the variable from the equations. Also, if they feel it is redundant to use \[\left( h,k \right)\]first and then replace it as \[\left( x,y \right)\] they may use \[\left( x,y \right)\]from the start as well.