Question

Find the locus of the middle points of chords of the parabola which are normal to the curve.

Answer 1

Hint: Write the equation of normal to the parabola at a general point on it and see where it intersects the curve again. Find the midpoint.

Complete step-by-step answer:

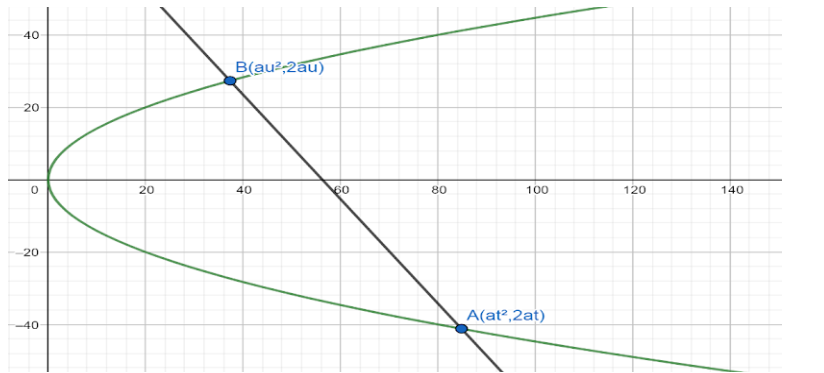
Consider the above picture. \[A\left( a{{t}^{2}},2at \right)\] and \[B\left( a{{u}^{2}},2au \right)\]are two variable points on the standard parabola \[{{y}^{2}}=4ax\] with parameters \[t\] and \[u\] respectively.
It is given that $AB$ is normal to the parabola at\[B\].
We can write equations for $AB$ using the formula for normals which is,
Normal at a point with parameter (\[t\]) is given by,
\[y+tx=2at+a{{t}^{3}}\]
So we get the equation of line \[AB\] as,
\[AB:y+ux=2au+a{{u}^{3}}\]
We know that normal to the parabola at point with parameter \[t\] cuts it again at another point with parameter$-t-\dfrac{2}{t}$.
We can prove this by solving the equation of normal i.e. \[AB\] and parabola together.
So we get point\[A\]as,
$A=\left( a{{\left( -t-\dfrac{2}{t} \right)}^{2}},2a\left( -t-\dfrac{2}{t} \right) \right)$
Now let point \[\left( h,k \right)\]lie on our locus. Since they lie on the locus it is the midpoint of our variable chord\[AB\].
So using the midpoint formula which is,
Xmid=\[\dfrac{x1+x2}{2}\]
ymid= \[\dfrac{y1+y2}{2}\]
We write,
$h=\left\{ \dfrac{\left( x~coordinate~of~A \right)+\left( x~coordinate~of~B \right)}{2} \right\}$
$k=\left\{ \dfrac{\left( y~coordinate~of~A \right)+\left( y~coordinate~of~B \right)}{2} \right\}$
And,
$h=\left\{ \dfrac{\left( \text{a}{{\text{t}}^{2}} \right)+\left( a{{\left( -t-\dfrac{2}{t} \right)}^{2}} \right)}{2} \right\}$
$2h=\left( \text{a}{{\text{t}}^{2}} \right)+\left( a{{\left( -t-\dfrac{2}{t} \right)}^{2}} \right)$
\[\dfrac{2h}{a}={{\text{t}}^{2}}+{{\left( -t-\dfrac{2}{t} \right)}^{2}}\]
\[\dfrac{2h}{a}={{\text{t}}^{2}}+\left( {{\left( -t \right)}^{2}}+{{\left( -\dfrac{2}{t} \right)}^{2}}+2(-t)\left( -\dfrac{2}{t} \right) \right)\]
\[\dfrac{2h}{a}=2{{t}^{2}}+\dfrac{4}{{{t}^{2}}}+4\]
\[\dfrac{h}{a}={{t}^{2}}+\dfrac{2}{{{t}^{2}}}+2...(i)\]
$k=\left\{ \dfrac{\left( 2at \right)+\left( 2a\left( -t-\dfrac{2}{t} \right) \right)}{2} \right\}$
$2k=\left( 2at \right)+\left( 2a\left( -t-\dfrac{2}{t} \right) \right)$
$\dfrac{2k}{a}=2t+2\left( -t-\dfrac{2}{t} \right)$
$\dfrac{2k}{a}=\dfrac{-4}{t}$
$t=\dfrac{-2a}{k}...(ii)$
So our next task in finding the locus is eliminating the variables from the above equations.
Substituting equation \[\left( ii \right)\] in \[\left( i \right)\] we get,
$\dfrac{h}{a}={{\left( \dfrac{-2a}{k} \right)}^{2}}+\dfrac{2}{{{\left( \dfrac{-2a}{k} \right)}^{2}}}+2$
$\dfrac{h}{a}={{\left( \dfrac{-2a}{k} \right)}^{2}}+2{{\left( \dfrac{k}{-2a} \right)}^{2}}+2$
$\dfrac{h}{a}=\dfrac{4{{a}^{2}}}{{{k}^{2}}}+2\dfrac{{{k}^{2}}}{4{{a}^{2}}}+2$
$\dfrac{h}{a}=\dfrac{4{{a}^{2}}}{{{k}^{2}}}+\dfrac{{{k}^{2}}}{2{{a}^{2}}}+2$
$h=\dfrac{4{{a}^{3}}}{{{k}^{2}}}+\dfrac{{{k}^{2}}}{2a}+2$
This is the required locus.
Now since \[\left( h,k \right)\]are general points on our locus we can replace \[h\] by \[x\] and \[k\] by \[y\].
$x=\dfrac{4{{a}^{3}}}{{{y}^{2}}}+\dfrac{{{y}^{2}}}{2{{a}}}+2$
This is the required locus.

Note: Students have to think carefully while deciding which is the variable before eliminating. In this question students might eliminate \[a\] which will give them the wrong answer. Also they may use their different techniques to eliminate the variable from the equations. Also, if they feel it is redundant to use \[\left( h,k \right)\]first and then replace it as \[\left( x,y \right)\]they may use \[\left( x,y \right)\]from the start as well.