Question

Find the locus of a point O when three normals are drawn from it are such that one bisects the angle between the other two.

Answer 1

Hint: Take a general point inside the parabola and draw three normals from that point. Angles between the middle one and the extreme ones should be equal as it bisects them.

Complete step-by-step answer:
Let us first draw a diagram with the details given in the question.

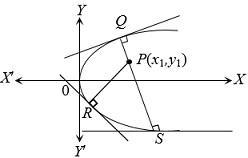
From point \[P\] three normals \[(PR,PS,PQ)\] are drawn to the parabola \[{{y}^{2}}=4ax\]. Equation of a general normal to the parabola \[{{y}^{2}}=4ax\] is \[y=mx-2am-a{{m}^{3}}\], where \[m\] is the slope of the normal.
So we write the equation of the normal as,
\[{{y}_{1}}=m{{x}_{1}}-2am-a{{m}^{3}}\]
\[a{{m}^{3}}+2am-m{{x}_{1}}+{{y}_{1}}=0...(i)\]
Equation \[\left( i \right)\] is a cubic equation in \[m\] with roots \[{{m}_{1}},{{m}_{2}},{{m}_{3}}\]. It is given that $\angle RPS=\angle RPQ$. So we can write,
$\dfrac{{{m}_{3}}-{{m}_{2}}}{1+{{m}_{3}}\times {{m}_{2}}}=\dfrac{{{m}_{2}}-{{m}_{1}}}{1+{{m}_{2}}\times {{m}_{1}}}$
\[\left( {{m}_{3}}-{{m}_{2}} \right)\left( 1+{{m}_{2}}\times {{m}_{1}} \right)=\left( {{m}_{2}}-{{m}_{1}} \right)\left( 1+{{m}_{3}}\times {{m}_{2}} \right)\]
\[{{m}_{3}}\left( 1+{{m}_{2}}\times {{m}_{1}} \right)-{{m}_{2}}\left( 1+{{m}_{2}}\times {{m}_{1}} \right)={{m}_{2}}\left( 1+{{m}_{3}}\times {{m}_{2}} \right)-{{m}_{1}}\left( 1+{{m}_{3}}\times {{m}_{2}} \right)\]
\[{{m}_{3}}+{{m}_{1}}\times {{m}_{2}}\times {{m}_{3}}-{{m}_{2}}-{{m}_{1}}{{\left( {{m}_{2}} \right)}^{2}}={{m}_{2}}+{{m}_{3}}{{({{m}_{2}})}^{2}}-{{m}_{1}}-{{m}_{1}}\times {{m}_{2}}\times {{m}_{3}}\]
\[{{m}_{3}}+{{m}_{1}}-2{{m}_{2}}+2{{m}_{1}}\times {{m}_{2}}\times {{m}_{3}}-{{\left( {{m}_{2}} \right)}^{2}}\left( {{m}_{1}}+{{m}_{3}} \right)=0.....(ii)\]
Also from equation \[\left( i \right)\] we get, the product and sum of roots as,
\[{{m}_{1}}{{m}_{2}}{{m}_{3~~}}=~\dfrac{-{{y}_{1}}}{a}...(iii)\]
\[{{m}_{1}}+{{m}_{2}}+{{m}_{3}}=0\]
\[-{{m}_{2}}=\text{ }{{m}_{1}}+{{m}_{3}}...(iv)\]
Substituting equations \[\left( iii \right),\left( iv \right)\] in \[\left( ii \right)\] we get,
\[-{{m}_{2}}-2{{m}_{2}}+2\left( \dfrac{-{{y}_{1}}}{a} \right)-{{\left( {{m}_{2}} \right)}^{2}}\left( -{{m}_{2}} \right)=0\]
${{\left( {{m}_{2}} \right)}^{3}}=3{{m}_{2}}+\dfrac{2{{y}_{1}}}{a}...(v)$
Since we know that the roots satisfy the equation, we can substitute equation \[\left( v \right)\] in \[\left( i \right)\],
$a\left( 3{{m}_{2}}+\dfrac{2{{y}_{1}}}{a} \right)+2a{{m}_{2}}-\left( {{m}_{2}}\times {{x}_{1}} \right)+{{y}_{1}}=0$
$3a{{m}_{2}}+2{{y}_{1}}+2a{{m}_{2}}-\left( {{m}_{2}}\times {{x}_{1}} \right)+{{y}_{1}}=0$
$5a{{m}_{2}}+3{{y}_{1}}-\left( {{m}_{2}}\times {{x}_{1}} \right)=0$
$3{{y}_{1}}-{{m}_{2}}\left( {{x}_{1}}-5a \right)=0$
$3{{y}_{1}}={{m}_{2}}({{x}_{1}}-5a)$
\[{{m}_{2~}}=\dfrac{3{{y}_{1}}}{{{x}_{1}}-5a}...(vi)\]
Substituting equation \[\left( vi \right)\] in \[\left( v \right)\] we get,
 \[\begin{align}
  & {{\left( \dfrac{3{{y}_{1}}}{{{x}_{1}}-5a} \right)}^{3}}=3\left( \dfrac{3{{y}_{1}}}{{{x}_{1}}-5a} \right)+\dfrac{2{{y}_{1}}}{a} \\
 & {{\left( \dfrac{3{{y}_{1}}}{{{x}_{1}}-5a} \right)}^{3}}-\left( \dfrac{9{{y}_{1}}}{{{x}_{1}}-5a} \right)-\dfrac{2{{y}_{1}}}{a}=0 \\
 & \dfrac{27{{y}_{1}}^{3}}{{{\left( {{x}_{1}}-5a \right)}^{3}}}-\dfrac{9{{y}_{1}}}{{{x}_{1}}-5a}-\dfrac{2{{y}_{1}}}{a}=0 \\
\end{align}\]
Taking out common terms, we get
\[\dfrac{27{{y}_{1}}^{2}}{{{\left( {{x}_{1}}-5a \right)}^{3}}}-\dfrac{9}{{{x}_{1}}-5a}-\dfrac{2}{a}=0\]
Taking the LCM of terms, we get
\[\begin{align}
  & \dfrac{27a{{y}_{1}}^{2}-9a{{\left( {{x}_{1}}-5a \right)}^{2}}-2{{\left( {{x}_{1}}-5a \right)}^{3}}}{a{{\left( {{x}_{1}}-5a \right)}^{3}}}=0 \\
 & 27a{{y}_{1}}^{2}-9a{{\left( {{x}_{1}}-5a \right)}^{2}}-2{{\left( {{x}_{1}}-5a \right)}^{3}}=0 \\
\end{align}\]
Using the expansions \[{{\left( a-b \right)}^{2}}={{a}^{2}}-2ab+{{b}^{2}}\] and ${{\left( a-b \right)}^{3}}={{a}^{3}}-{{b}^{3}}-3ab\left( a-b \right)$, we get
\[\begin{align}
  & 27a{{y}_{1}}^{2}-9a\left( {{x}_{1}}^{2}-10a{{x}_{1}}+25{{a}^{2}} \right)-2\left( {{x}_{1}}^{3}-125{{a}^{3}}-15a{{x}_{1}}\left( {{x}_{1}}-5a \right) \right)=0 \\
 & 27a{{y}_{1}}^{2}-9a\left( {{x}_{1}}^{2}-10a{{x}_{1}}+25{{a}^{2}} \right)-2\left( {{x}_{1}}^{3}-125{{a}^{3}}-15a{{x}_{1}}^{2}+75{{a}^{2}}{{x}_{1}} \right)=0 \\
 & 27a{{y}_{1}}^{2}-9a{{x}_{1}}^{2}+90{{a}^{2}}{{x}_{1}}-225{{a}^{3}}-2{{x}_{1}}^{3}+250{{a}^{3}}+30a{{x}_{1}}^{2}-150{{a}^{2}}{{x}_{1}}=0 \\
 & -2{{x}_{1}}^{3}+21a{{x}_{1}}^{2}-60{{a}^{2}}{{x}_{1}}+25{{a}^{3}}+27a{{y}_{1}}^{2}=0 \\
\end{align}\]
This is the required locus. Now since \[\left( {{x}_{1}},{{y}_{1}} \right)\] are general points on our locus, we can replace \[{{x}_{1}}\] by \[x\] and \[{{y}_{1}}\] by \[y\]. So, we will get
\[\begin{align}
  & -2{{x}^{3}}+21a{{x}^{2}}-60{{a}^{2}}x+25{{a}^{3}}+27a{{y}^{2}}=0 \\
 & \Rightarrow 2{{x}^{3}}-21a{{x}^{2}}+60{{a}^{2}}x-27a{{y}^{2}}-25{{a}^{3}}=0 \\
\end{align}\]
This is the required locus.
Note: Students have to think carefully while deciding which is the variable before eliminating. In this question, students might eliminate \[a\] which will give them the wrong answer. Also, they may use different techniques to eliminate the variable from the equations. If they feel it is redundant to use \[\left( {{x}_{1}},{{y}_{1}} \right)\] first and then replace it as \[\left( x,y \right)\], they may use \[\left( x,y \right)\] from the start as well.